Was ist eine lineare Funktionsgleichung?

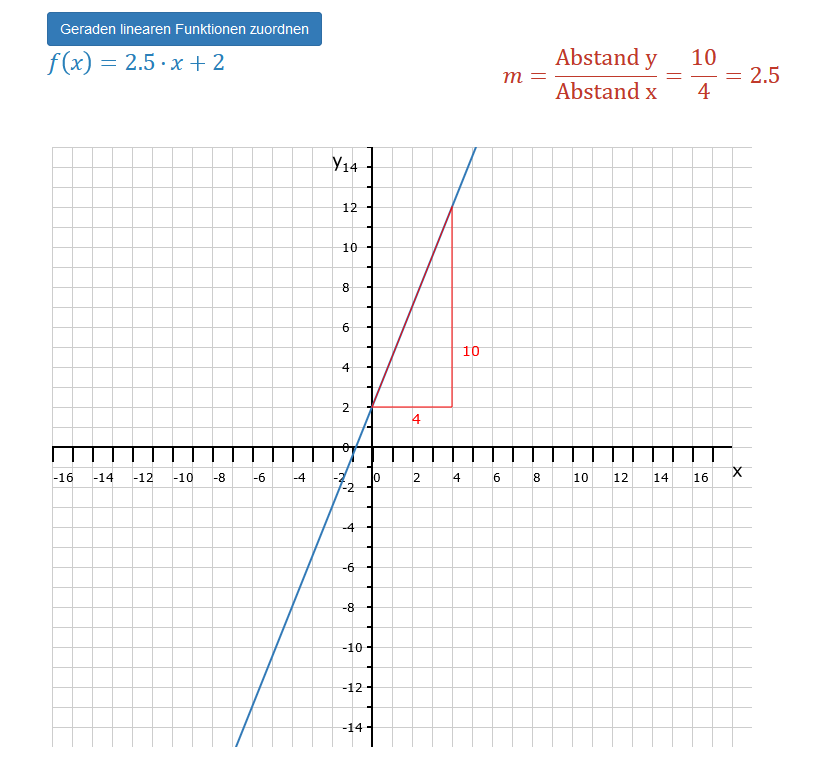
Eine lineare Funktion ist wie eine kleine Maschine, in die man einen Wert x gibt. Dieser Wert durchläuft einen bestimmten Rechenprozess. Dieser wird bestimmt durch einen Term, der gewisse Bedingungen erfüllen muss. Vor dem x gibt es einen sogenannten Steigungsfaktor m und hinter dem x ein Absolutglied b, auch Konstante b genannt. Das Ergebnis dieses Terms ist ein Wert, den wir Funktionswert y nennen. Die allgemeine Form dieser Funktion sieht demnach so aus: f(x) = m · x + b

Dadurch, dass es zu jedem x-Wert einen "errechneten" y-Wert gibt, der einer durch den Funktionsterm bestimmten festen Regel unterliegt, der Funktionsvorschrift, gibt es zu jedem x eine feste Zuordnung y. Damit lösen wir uns zum ersten Mal vom Zahlenstrahl und begeben uns in die zweidimensionale Welt der Funktionen. Diese Welt wird von Punkten bevölkert. Jeder Punkt hat eine Koordinate, die exakt seine Position auf einer Fläche bestimmt, die sich in einem Koordinatensystem befindet. Was ist ein Koordinatensystem?

Ein Koordinatensystem besteht aus 2 Achsen, der x-Achse und der y-Achse. Beide Achsen weisen eine sogenannte Skalierung auf. Befinden wir uns in einem kleineren Wertebereich, sagen wir bis 15 oder 20, ist es sinnvoll, für beide Achsen die gleiche Skalierung zu verwenden (siehe Bild). Zur Bestimmung der Position eines Punktes lesen wir auf der x-Achse den Wert für x ab und fahren dann mit dem Finger hoch, bis wir auf der Höhe des Wertes für y sind, den wir an der y-Achse ablesen können. Dadurch, dass jeder Punkt einer Funktion der gleichen Funktionsvorschrift unterliegt, ergeben alle Punkte, und das sind unendlich viele, eine Gerade, deren Steigung, Gefälle, Höhe oder Tiefe von den Parametern m und b abhängig ist.

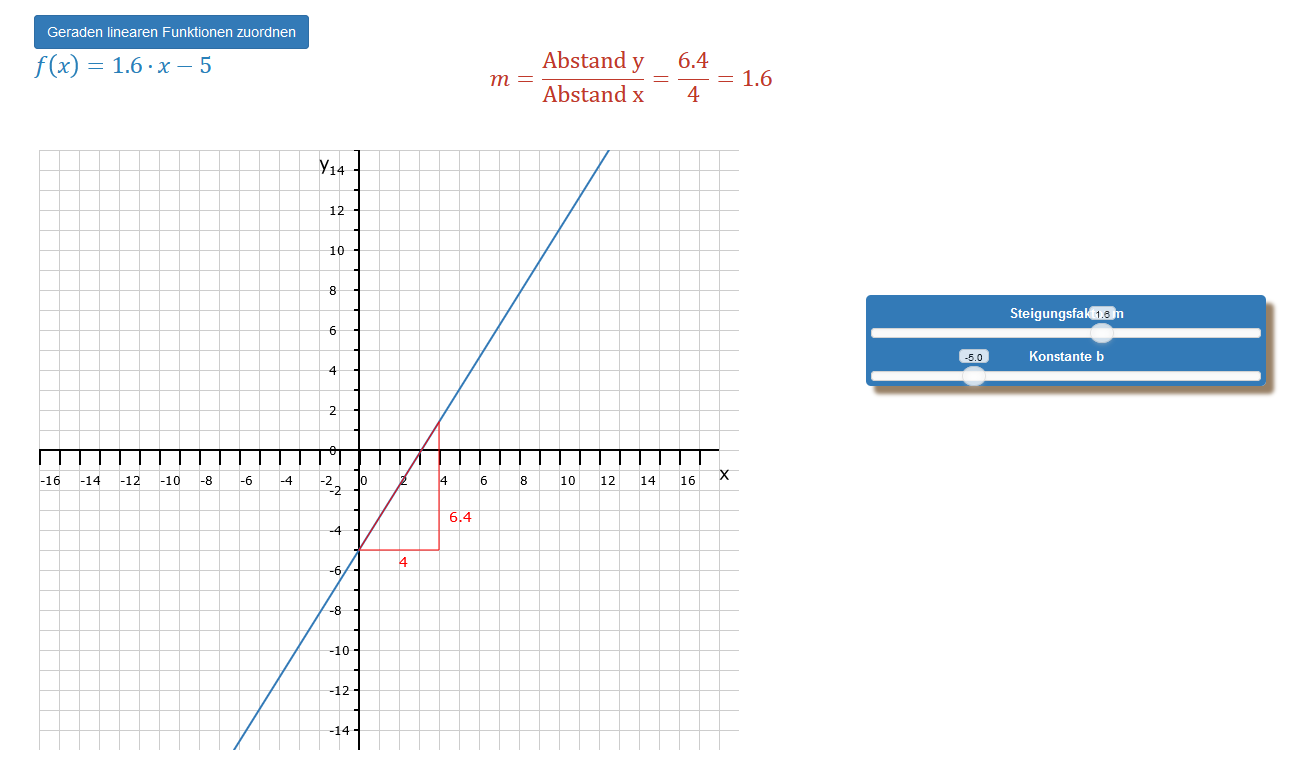
In unserer interaktiven App kannst Du nun mithilfe von Schiebereglern spielerisch ausprobieren, wie sich die Ausrichtung und Position der Geraden verändert, wenn Du die Regler für den Steigungsfaktor m oder den für die Konstante b durch Schieben veränderst.

Gleichzeitig verändern sich die Werte in der Funktionsgleichung links oben. Rechts daneben befindet sich die Formel zur Berechnung des Steigungsfaktors m. Der Wert für m berechnet sich aus dem sogenannten Steigungsdreieck, das Du in dem Bild rot dargestellt siehst. Wie zeichnest Du das Steigungsdreieck ins Koordinatensystem? Der Schnittpunkt der Geraden auf der y-Achse liegt bei -2,5. In diesem Fall muss der x-Wert bei 0 liegen. Das heißt, wenn x = 0 ist, dann wird das Produkt m · x zu Null und folglich ist y = b. Nun nimmst Du einen beliebigen Wert für x, wir haben hier 4 genommen, und trägst eine Strecke vom Schnittpunkt bis 4 Einheiten nach rechts ab. Nun nimmst Du das 1,6 Fache von 4, das sind 6,4, und zeichnest die senkrechte Seite des Steigungsdreiecks ein. Die Hypotenuse dieses Dreiecks ist eine Teilstrecke unserer Geraden. Ist der y-Abstand größer als der x-Abstand, wird die Gerade steiler, also m ist dann größer als 1. Im umgekehrten Fall ist die Ausrichtung der Geraden flacher. Hier liegt der Wert für m zwischen 0 und 1.

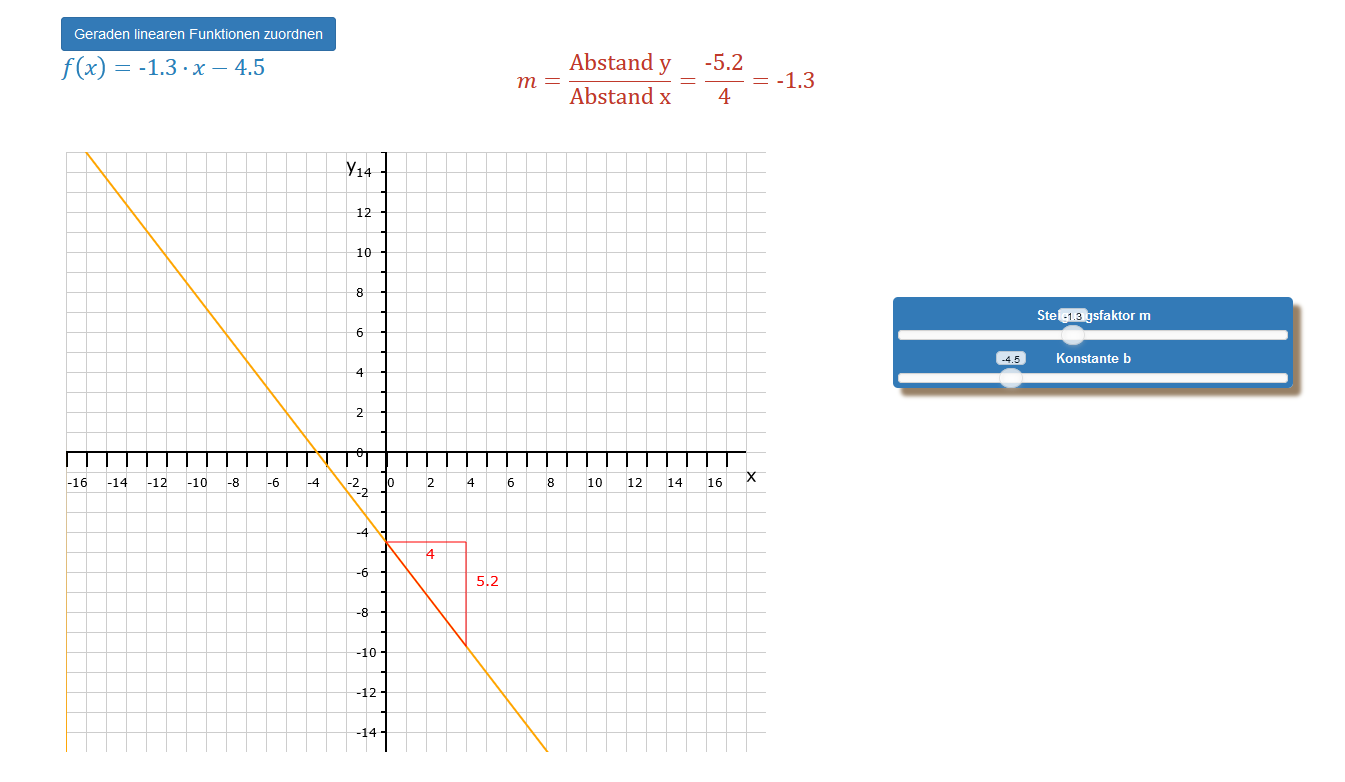
Im nebenstehenden Bild siehst Du ein Beispiel für eine fallende Gerade. Die App zeichnet steigende Geraden blau und fallende Geraden orange. Was ist hier anders als im ersten Bild? In der Funktionsgleichung kann man bereits erkennen, dass der Steigungsfaktor m, auch Koeffizient genannt, negativ ist. Bei einer steigenden Geraden musst Du Dir vorstellen, dass es einen Anfangswert gibt, der durch b definiert wird, denn wenn x = 0, dann ist y = b. Durch die Multiplikation von x größer als Null mit einem Koeffizienten größer als Null steigt dieser Anfangswert. Also mit jeder Zunahme von x steigt auch der Anfangswert von y, was zu einer Steigung der Geraden führt. Je größer m ist, umso steiler steigt der y-Wert.

Ist der Koeffizient negativ, so wird mit jeder Einheit von x der entsprechende y-Wert vom Anfangswert abgezogen, denn dann haben wir y = b - m · x. Für das Steigungsdreieck bedeutet das, dass wir jetzt die Dreiecksseite für den y-Abstand nicht nach oben, in den positiven Bereich, sondern nach unten, in den negativen Bereich zeichnen.