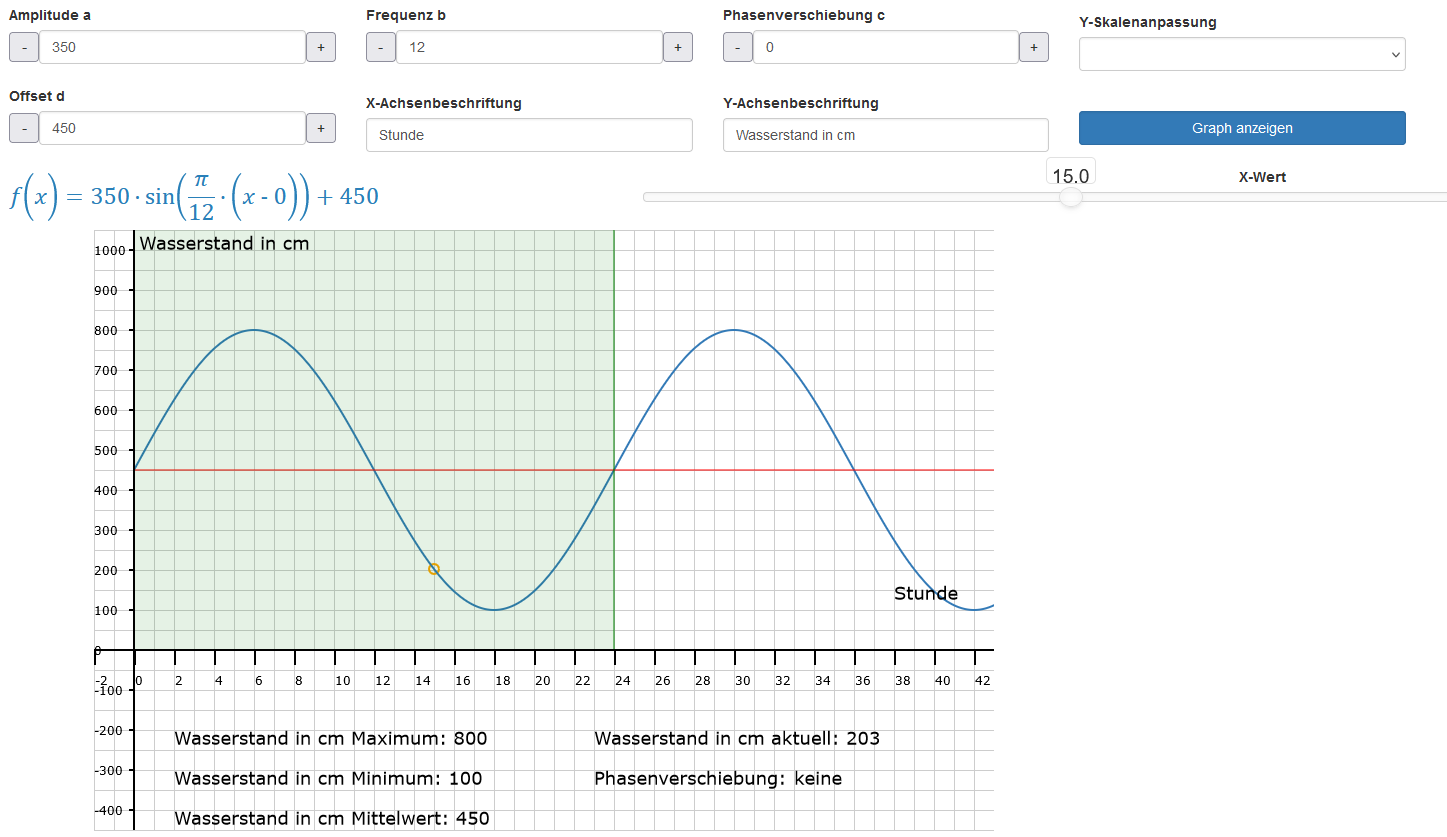
So modellierst Du Sinusfunktionen!
Die allgemeine Form der Sinusfunktion lautet: .
Sie weist 4 Parameter auf. Ihr Einfluss auf Lage und Form des Graphen wird im Folgenden erklärt. Der Faktor a ist für die Amplitude verantwortlich. Das ist der Ausschlag der Sinuswelle nach oben und nach unten, gemessen von der Mittelwertslinie aus. Eine Amplitude von 5 umfasst bei einem Mittelwert von beispielsweise 10 einen Bereich von 5 bis 15. Die Amplitude beschreibt also die maximale Entfernung des Funktionswerts vom Mittelwert (Gleichgewichtslage) der Sinuskurve.
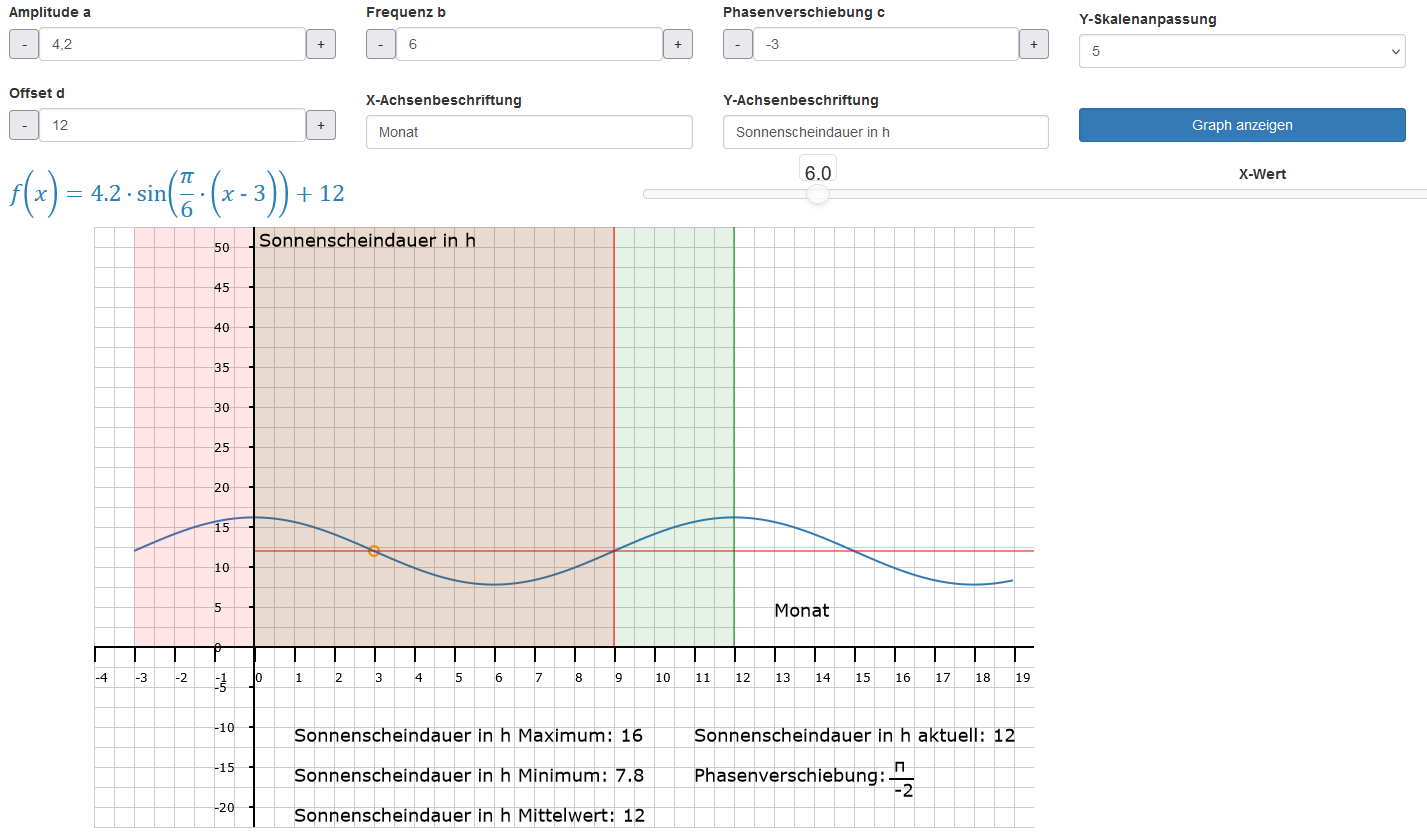
Der Faktor b beschreibt die Frequenz der Sinuskurve. Die Beispielfunktion, die den Graphen links im Bild erzeugt, lautet: . Der Frequenzfaktor beeinflusst die Länge der Periode. Sie beträgt immer 2 · π. Weist π keinen Nenner auf, beginnt die Kurve beim Mittelwert, durchläuft den Höchstpunkt und schneidet wieder die Mittelwertslinie bei x = 1. Dann durchläuft sie den Tiefstwert und strebt wieder der Mittelwertslinie zu. Sie schneidet sie bei x = 2. Die Distanz entlang der x-Achse beträgt also 2 Einheiten. Die Periodenlänge T beträgt demnach 2.
In unserem Beispiel haben wir im Nenner eine 6 stehen. Wenn in der Normalform die π-Distanz eine Einheit umfasst, sind es hier 6. Nachdem die Periode über eine Distanz von 2 · π geht ist T = 12. Der hellgrün gefärbte Bereich reicht auf der x-Achse bis zum Wert 12.
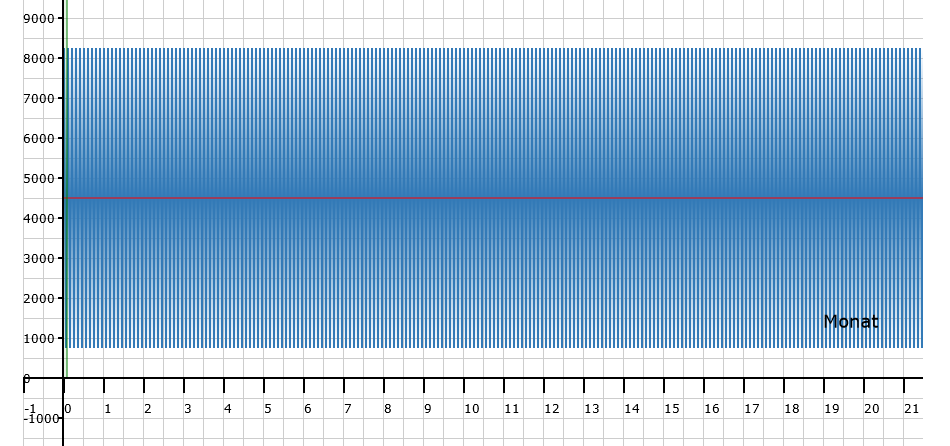
Je größer T ist, umso niedriger ist die Frequenz. Die Anzahl der Wellen verringert sich. Umgekehrt vergrößert sich die Zahl, wenn b kleiner Eins jedoch größer Null ist. In diesem Bild könnt ihr erkennen, was passiert, wenn ihr in die App für b zum Beispiel 0,05 eingebt. Die grün gefärbte Periode hat sich zu einem Strich verengt.
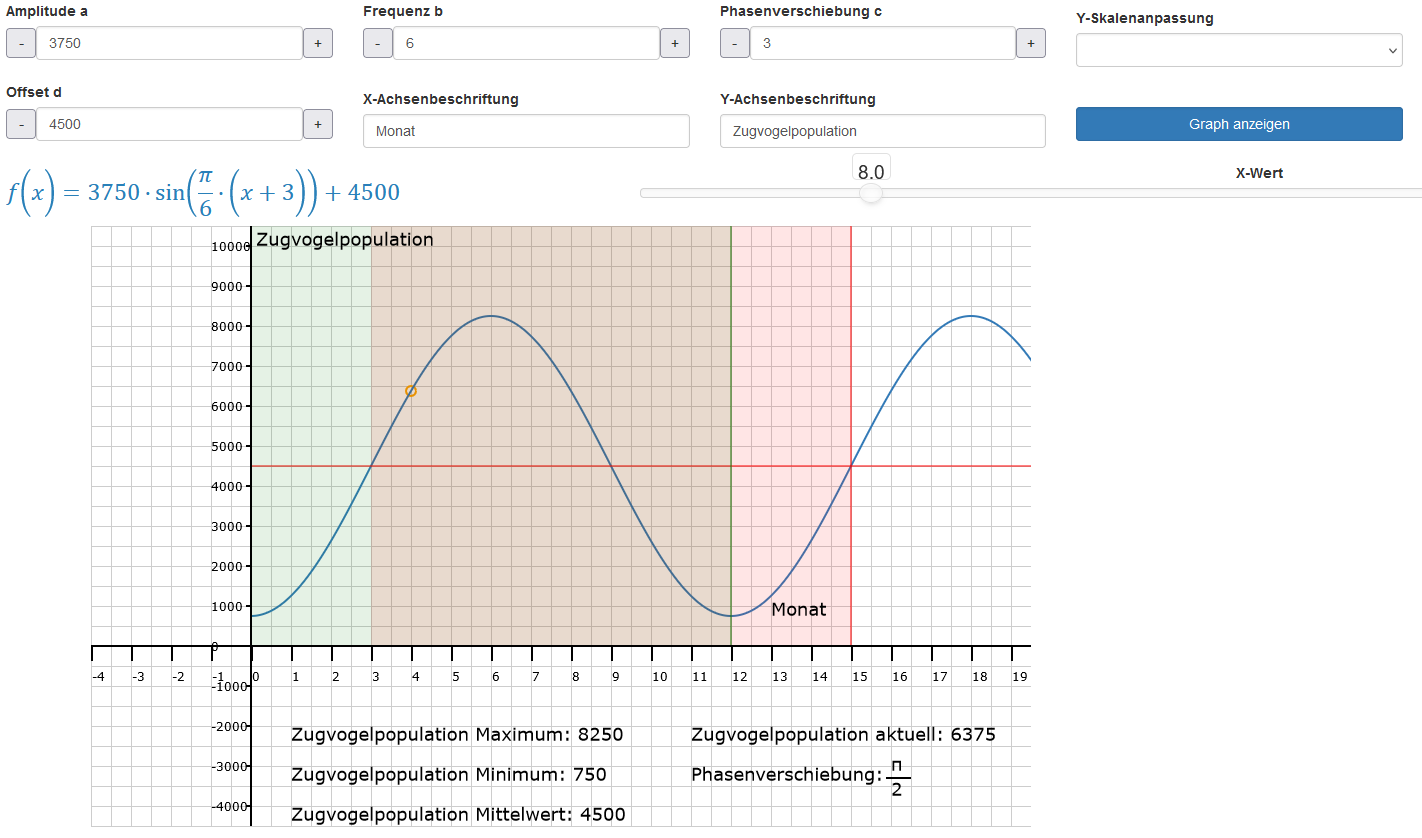
Im linken Bild sehen wir die Modellierungs-App, die wir mit Daten aus einer Anwendungsaufgabe gefüttert haben, bei der es um die zyklische Zu- und Abnahme einer Zugvogelpopulation über einen Beobachtungszeitraum von einem Jahr geht. Auch hier haben wir für den Frequenzfaktor b eine 6 eingetragen, da sich bei einem Beobachtungszeitraum von 12 Monaten eine Periode von T = 12 anbietet. Die Funktion, die die App erstellt lautet:
Ein weiterer Hinweis in der Aufgabe lautet, dass die Population im Juni ihr Maximum erreicht. Also müssen wir die Sinuskurve horizontal so verschieben, dass die Periode ab dem Beobachtungszeitpunkt Januar mit dem Minimum beginnt, um dann im Juni, das ist auf der x-Achse der Wert 6, das Maximum zu erreichen. Dafür ist der Parameter c für die Phasenverschiebung zuständig. Man kann die Periode in 4 Phasen zerlegen. Die erste Phase: der Anstieg vom Mittelwert, 0 im Einheitskreis, zum Maximum, 1 im Einheitskreis. Die zweite Phase: der Abstieg zum Mittelwert bzw. zu 0. In der 3. Phase ein Abstieg zum Minimum und die Rückkehr zum Mittelwert in der 4. Phase.
Wenn T = 12 ist und wir für den Parameter c eine 3 eingeben, weil es bis zum Maximum nicht 3, sondern 6 Monate braucht, dann verschiebt sich die Periode gemäß der Phasenverschiebung: . Also in unserem Beispiel: .
Nachdem der 4. Teil der Periodenlänge von 2 · π ist, findet eine Phasenverschiebung um statt, und weil c kein negatives Vorzeichen hat, erfolgt sie nach links. So beginnt die Sinuskurve nicht am Mittelwert, sondern um ein halbes π nach links versetzt beim ersten Minimum. Ein negatives c würde folglich die Periode nach rechts verschieben, wie wir es im ersten Bild sehen. Die rosafarbene Fläche ist immer die Sinusperiode von Mittelwert zu Mittelwert und die hellgrüne Fläche der phasenverschobene Beobachtungsabschnitt.