Die Sinusfunktion mit ihren Veränderungsparametern!

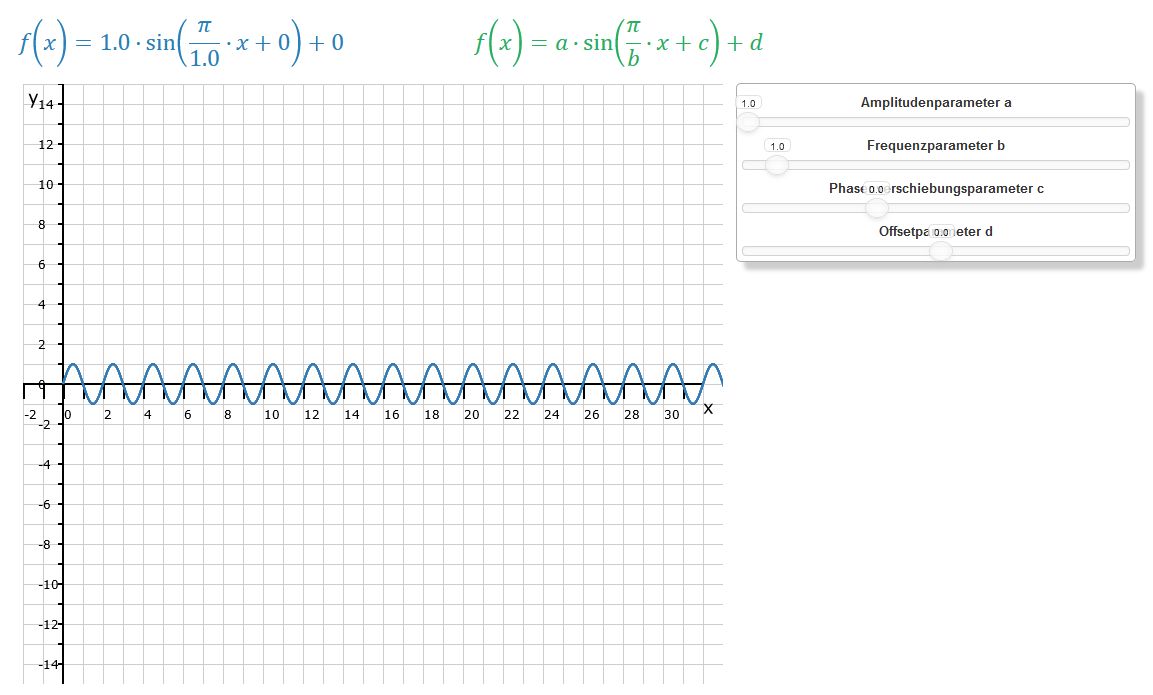
Wir nutzen unser bewährtes Koordinatensystem auch für die Sinusfunktion. Im nebenstehenden Bild siehst Du die Sinusfunktion in ihrer Normalform. Demnach ist $\mathrm{f(x)}=\sin (\pi ·x)$ Du siehst, dass die Sinuskurve mit der Amplitude 1, das entspricht dem Einheitskreis, eine Periode von T = 2 durchläuft. 2 Skalenstriche auf der x-Achse entsprechen also 2 π oder 360°. Hier können wir schon einmal die ersten beiden Parameter beschreiben.

Der Amplitudenparameter a = 1 und der Frequenzparameter b = 1. Da b gleich eins ist, entsprechen 1 Skalenschritt 180° und die Sinuskurve hat eine Periode von 2 Skalenstrichen oder 360°.

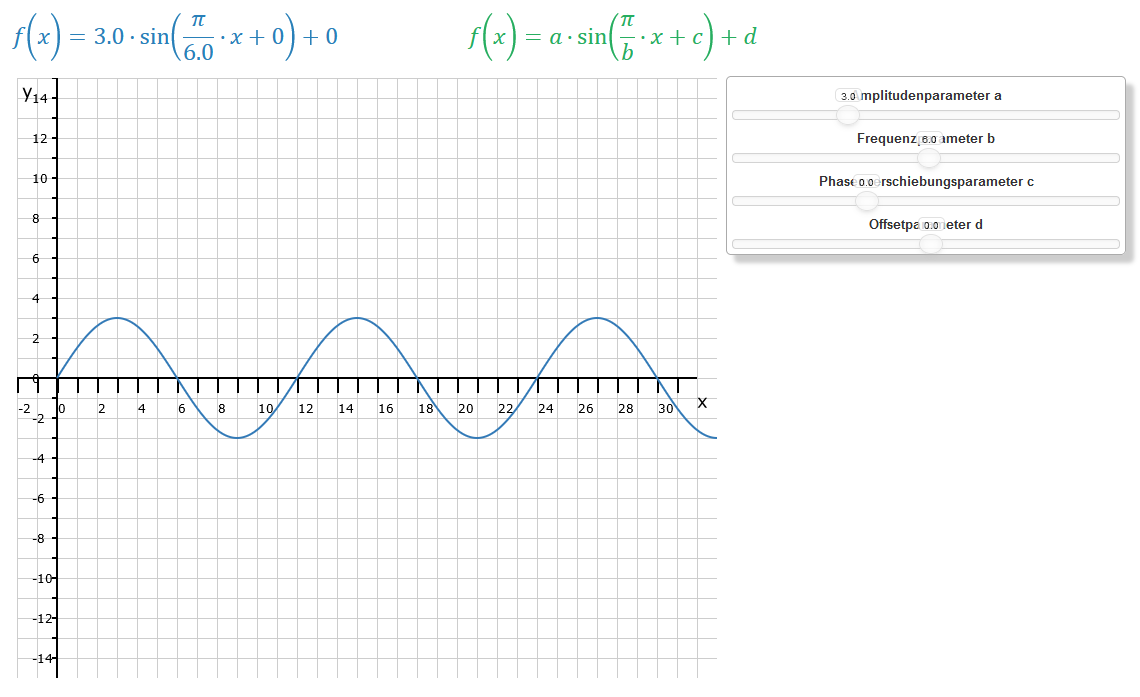
Wir erhöhen jetzt sowohl die Amplitude von 1 auf 3 als auch die Frequenz von 1 auf 6. Wie verändert sich die Sinuskurve? Zunächst ändert sich die Höhe des Ausschlags nach oben und nach unten von der x-Achse von 1 zu 3 bzw. von -1 zu -3. Durch die Veränderung des b-Parameters vergrößert sich die Periode auf T = 12. Wir haben jetzt folgende Funktion:

$\mathrm{f(x)}=3·\sin (\frac{\pi }{6}·x)$Die erste Nullstelle ist jetzt nicht mehr bei x = 1, sondern bei x = 6. Das wiederum entspricht π oder 180°. Daher entspricht die Periode von 360° auch 2 · π oder T = 12. Die Frequenz ist eine häufige Angabe in sogenannten Modellierungsaufgaben. Hier ist die x-Achse häufig die Zeitskala, an der man, um unser Beispiel mit T = 12 zu nehmen, eine periodische Zu- und Abnahme in einem Gesamtzeitraum von 12 Stunden ablesen kann. Dabei entspricht ein Skalenstrich auf der x-Achse $\frac{\pi }{6}$.

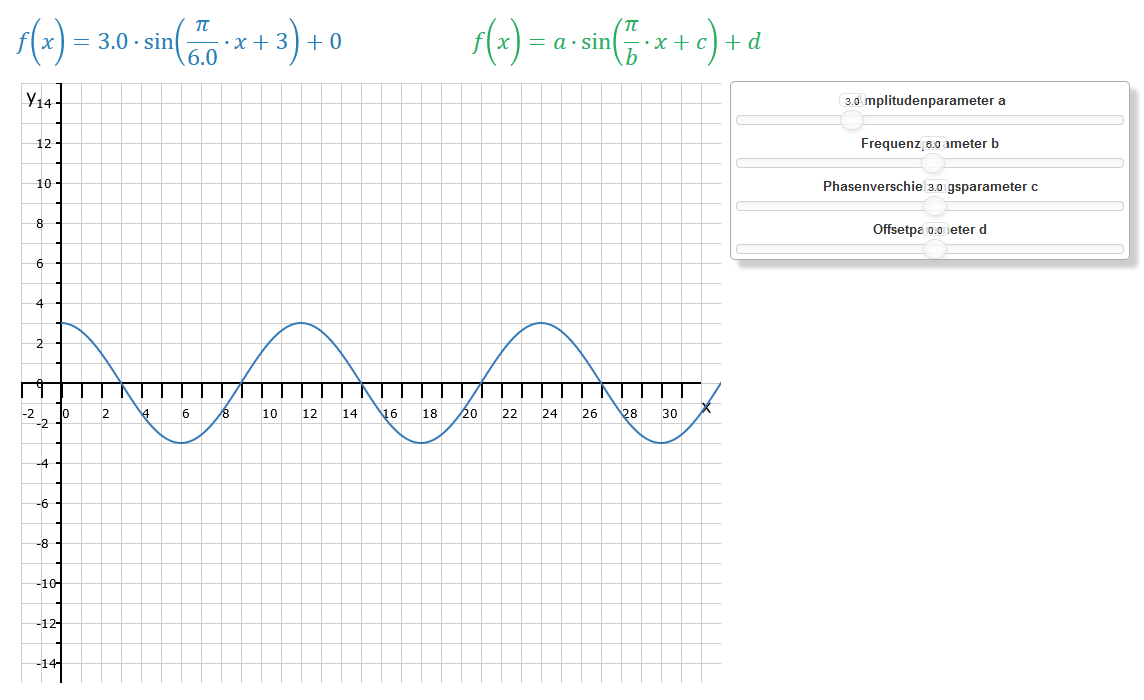
Wir behalten die bisherigen Einstellungen bei, verändern jetzt aber den Parameter c für die Phasenverschiebung. Was ist das? Wenn wir bisher die Höhe des Ausschlags, die Amplitude, und die Frequenz, die Zahl der x-Einheiten pro Periode, verändert haben, so verschieben wir nun die gesamte Funktion horizontal. In unserem Beispiel setzen wir c = 3 und erhalten die Funktion: $\mathrm{f(x)}=3·\sin (\frac{\pi }{6}·x+3)$. Mit der Addition der Konstanten c zu x verschieben wir die Wellenfunktion um 3 Einheiten nach links auf der x-Achse. Somit liegt die erste Nullstelle nun nicht mehr bei x = 6, sondern bei x = 3.



Mit dieser Änderung haben wir aus der Sinusfunktion eine Kosinusfunktion gemacht. Vom Einheitskreis wissen wir, dass wenn der Sinuswert bei 0° null ist, dann ist der Kosinuswert eins. Da man die Periode in vier Phasen einteilt, die jeweils eine Länge von $\frac{\pi }{2}$ haben, so wurde mit c = 3, die Periode T = 12 geteilt durch 4 (wegen der 4 Phasen) ergibt ja 3, die Funktion um eine Phase nach links verschoben. Die Linksverschiebung einer Phase macht aus der Sinusfunktion eine Kosinusfunktion. Anwendungsbeispiele gibt es, wenn der Beginn einer Periode nicht beim höchsten oder niedrigsten Stand ist, sondern irgendwo dazwischen. Das kann man mit der Konstanten c steuern.

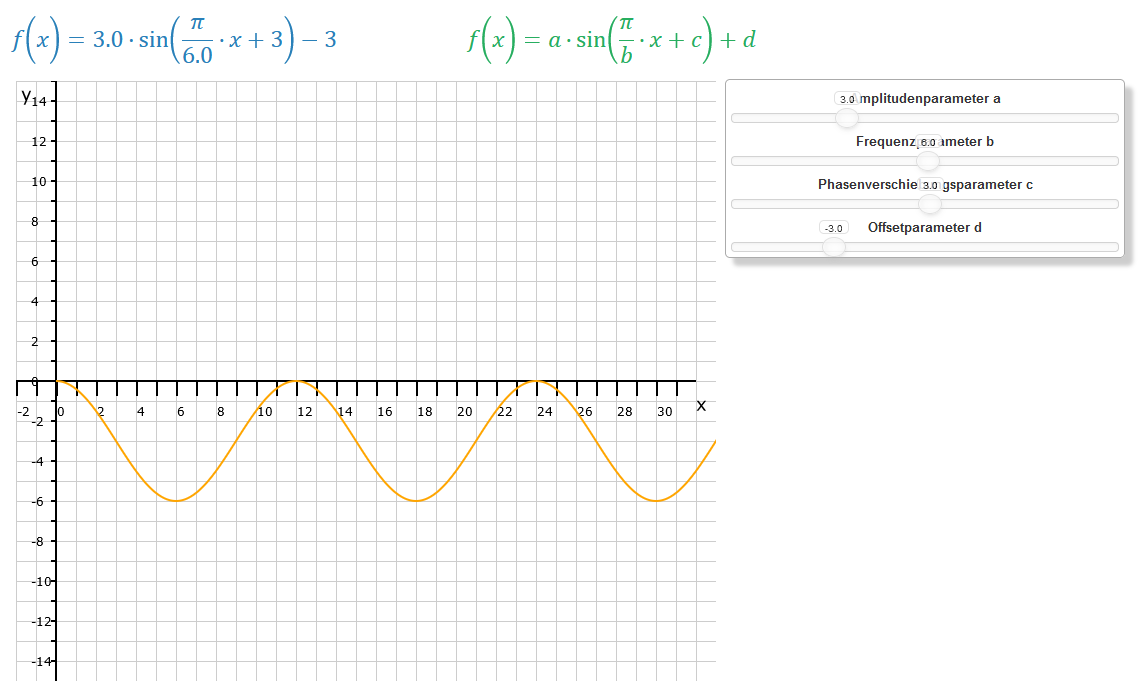
Zum Schluss verändern wir den 4. sogenannten Offset-Parameter d. Am nebenstehenden Bild kannst Du unschwer erkennen, dass die gesamte Funktion nach unten, also vertikal, verschoben wurde. Das ergibt die Funktionsgleichung: $\mathrm{f(x)}=3·\sin (\frac{\pi }{6}·x+3)-3$.
Mit dieser Änderung erreichen wir, dass sich die Mittelwertlinie, die standardmäßig von der x-Achse gebildet wird, je nach dem Vorzeichen von d nach oben oder nach unten verschiebt. Im Anwendungsfall geht es häufiger um eine Verschiebung in den positiven Bereich, wenn es z.B. um konkrete Höchst- oder Niedrigststände von Mengen geht, die ja bekanntlich nicht negativ sind.