Was ist eine quadratische Funktion?
Mit der linearen Funktion weißt Du inzwischen , was prinzipiell eine Funktion ist: Ein bestimmter Wert für x, dem ein Funktionswert y aufgrund einer sogenannten Funktionsvorschrift zugeordnet werden kann. Diese Zuordnungen kann man in eine Wertetabelle schreiben. Werte aus so einer Tabelle bilden die Koordinaten, um Punkte in ein Koordinatensystem einzutragen, deren Verbindung einen Graphen ergibt.
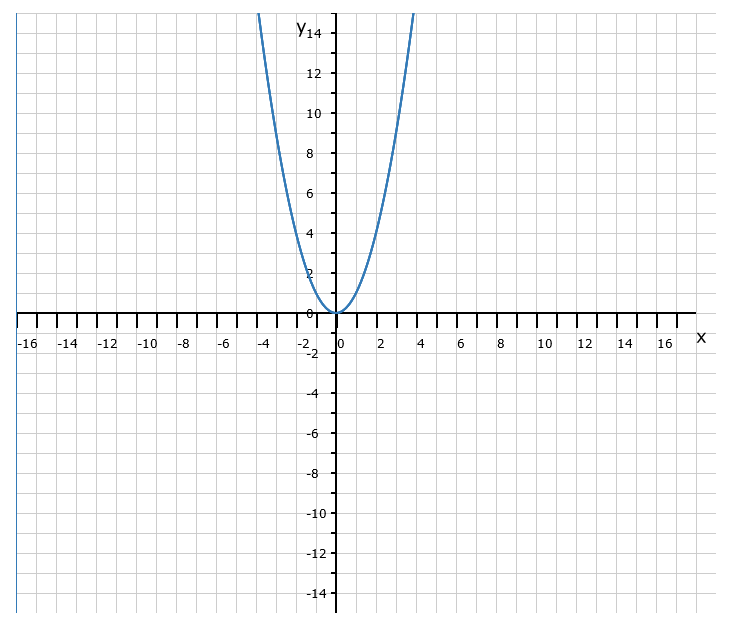
Bei der quadratischen Funktion lässt sich auch eine Wertetabelle mit Zuordnungen anlegen, nur dass der Wert für y nicht ein Vielfaches des Wertes von x ist, sondern das Quadrat von x. Ein wesentlicher Unterschied zwischen beiden Funktionen besteht darin, dass bei x² auch ein negatives x positiv wird.
Bei einer nicht verschobenen sogenannten Normalparabel f(x) = x² bedeutet das, dass der bei positivem x entstehende Graph eine stetig ansteigende Kurve bildet, deren tiefster Punkt, der Scheitelpunkt, im Ursprung liegt. Ist der x-Wert negativ, so bleibt der Funktionswert aber positiv und es bildet sich somit spiegelbildlich die gleiche ansteigende Kurve. Beide Kurven zusammen ergeben eine Parabel, wie Du sie in dem nebenstehenden Bild siehst.
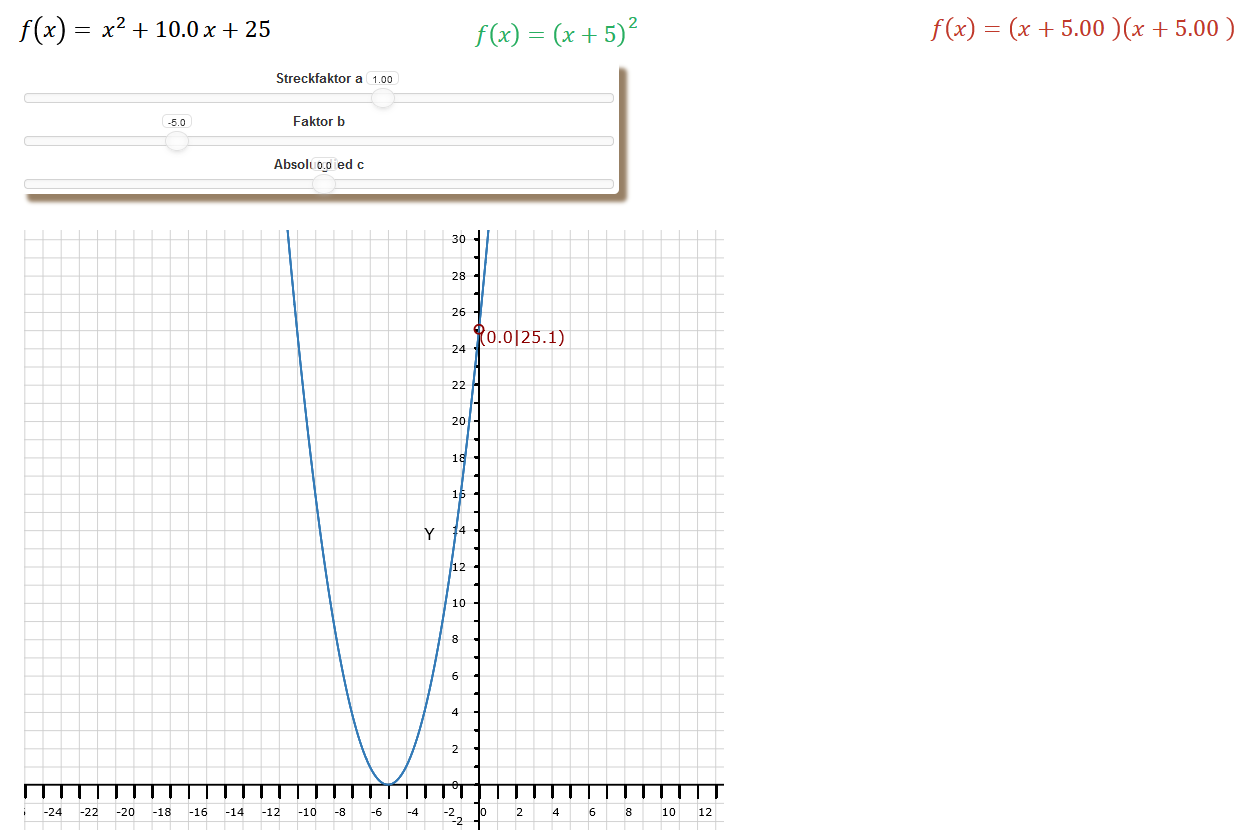
In unserer App hast Du nun 3 Schieberegler. Im Gegensatz zur linearen Funktion, bei der Du nur 2 Parameter hast, nämlich den Steigungsfaktor m und die Konstante b, hast Du bei der quadratischen Funktion 3 Parameter, und zwar a, b und c. Daher lautet die sogenannte Normalform der Funktion f(x) = ax² + bx + c.
Entsprechend sind unsere Schieberegler mit "Streckfaktor a", "Faktor b" und "Absolutglied c" beschriftet. Was bewirken Änderungen dieser 3 Parameter? Eine Änderung des Streckfaktors a staucht oder dehnt die Parabel. Ist a größer als 1, steigen die Schenkel der Parabel noch steiler an, der Abstand zwischen ihnen wird kleiner. Liegt der Wert zwischen 0 und 1, so vergrößert sich der Abstand zwischen den Parabelschenkeln, sie wird gedehnt. Eine Änderung des Koeffizienten b bewirkt, dass bei positivem b die Parabel nach links, also in den negativen x-Bereich verschoben wird und entsprechend bei negativem b in den positiven x-Bereich. Dabei senkt sich die Parabel so ab, dass entsprechend der rechte oder linke Schenkel der Parabel die Koordinatenachsen im Ursprung schneidet.
Um die Auswirkungen der einzelnen Parameter-Änderungen besser sichtbar zu machen, sind die Schieberegler so eingestellt, dass die Änderung von b nur zu einer horizontalen Verschiebung führt und die Änderung von c nur zu einer vertikalen. Im Bild oben links ist gut zu erkennen, dass eine horizontale Verschiebung um 5 Einheiten den y-Achsenabschnitt vom Ursprung Null auf 25 hochschnellen lässt, das Quadrat von 5.
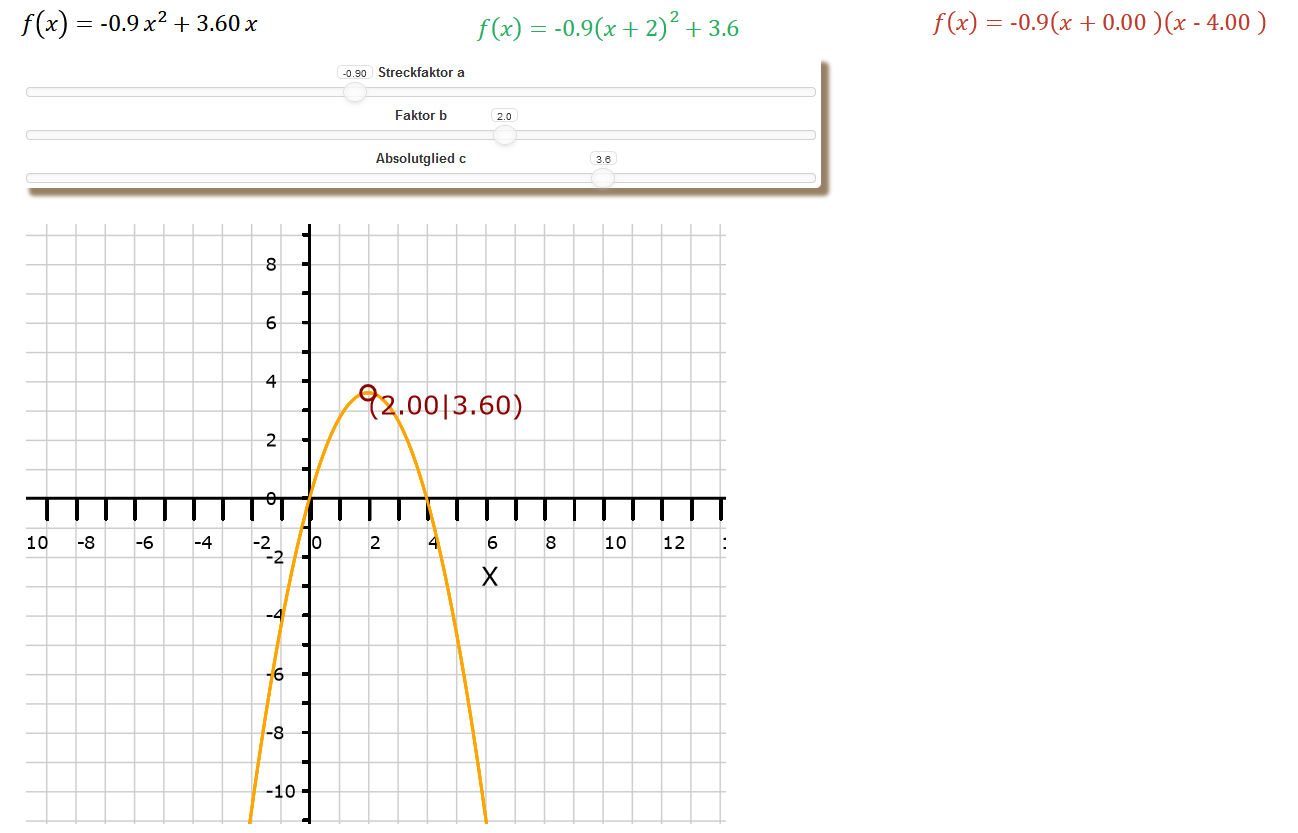
Oberhalb der Parabelzeichnung im Koordinatensystem siehst Du die Normalform der eingestellten Funktionsgleichung. Die Werte ändern sich dynamisch mit der Betätigung der Schieberegler. Rechts daneben siehst Du die Scheitelpunktform der Funktion. Ist b größer oder kleiner Null, wandelt sich das x² in dieser Form zur 1. oder 2. binomischen Formel. Das zeigt, dass bei y = 0, x den Wert annimmt, um die Klammer zu Null werden zu lassen. Das ist auch der Grund dafür, dass sich die Parabel horizontal immer in die zum Vorzeichen entgegengesetzte Richtung verschiebt.
Die 3. Funktionsform schließlich stellt eine sogenannte Linearfaktorzerlegung dar. Durch Ausmultiplizieren erhältst Du wieder die Normalform. Diese Form hat den Vorteil, dass Du quasi die Nullstellen ablesen kannst. Ein Vergleich der Werte, die x annimmt, um die Klammern zu Null werden zu lassen, mit den Schnittpunkten der Parabel an der x-Achse verdeutlichen das. Das funktioniert aber nur, wenn es 2 Nullstellen gibt. Andernfalls zeigt die App, dass eine Linearfaktorzerlegung nicht möglich ist.
Im nebenstehenden Bild siehst Du eine nach unten geöffnete Parabel, die ihren Scheitelpunkt in (2|3,6) hat und die Nullstellen bei 0 und 4. Diese Werte siehst Du auch in den obigen Funktionsformen. Der negative Streckfaktor von -0,9 führt zur nach unten geöffneten Parabel, die Scheitelpunktkoordinaten für x = 2 und y = 4, wobei das Vorzeichen in dem geklammerten Quadrat negativ sein müsste, aber positiv ist, da der negative Streckfaktor davor steht. Schließlich zeigt die Linearfaktorzerlegung die beiden Nullstellen bei 0 und 4 an, das heißt dass x die Werte 0 und 4 annehmen kann, damit der Funktionsterm zu Null wird.
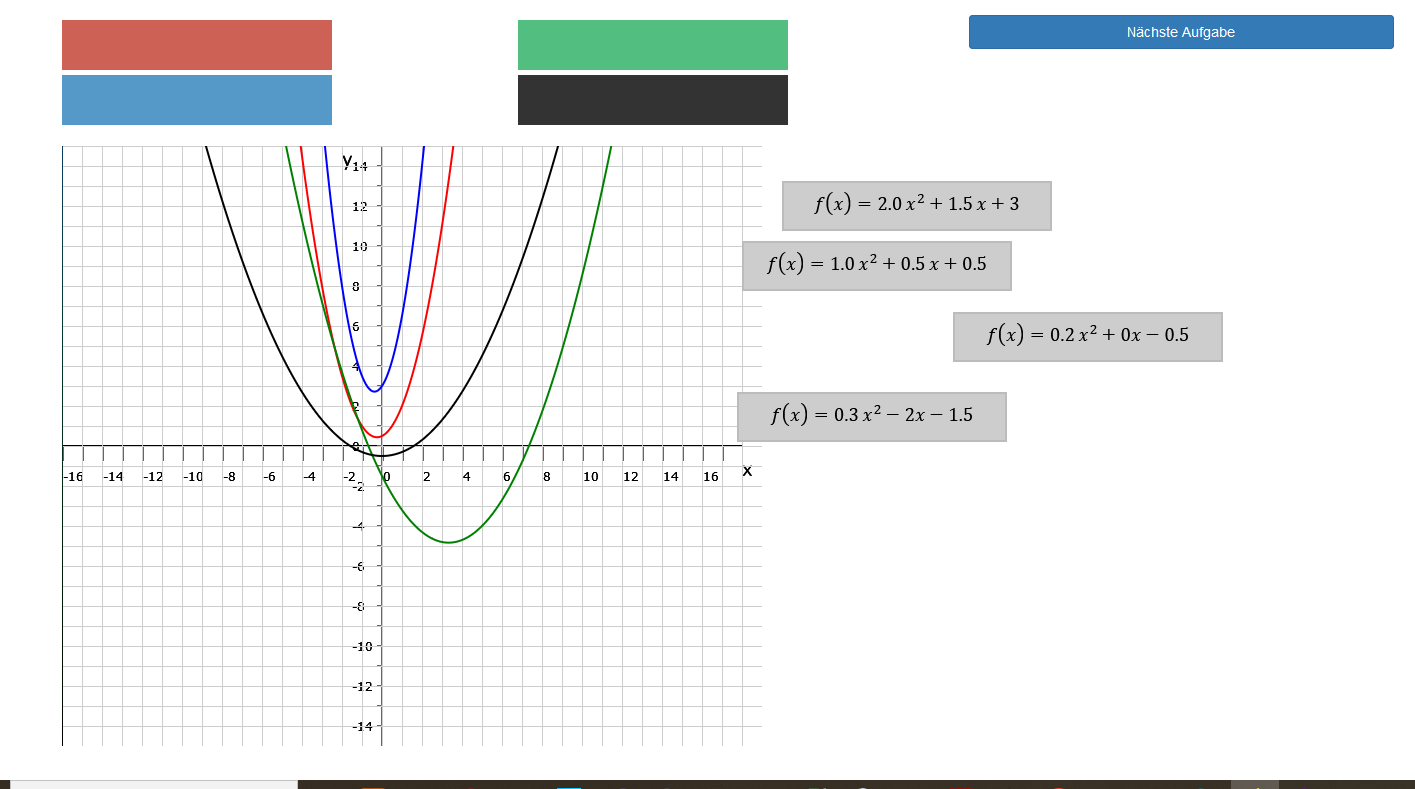
Zusätzlich gibt es in dieser App eine interaktive Übung, in der man 4 farblich unterschiedlichen Parabeln die entsprechenden Funktionsgleichungen zuordnen soll. In diesem Zusammenhang ist es noch wichtig zu erwähnen, dass ein negativer Dehnungsfaktor bewirkt, dass sich die Parabel nach unten, anstatt nach oben öffnet. Dieses und weitere Merkmale, die Du jetzt gelernt hast, sollten es Dir leicht machen, die passenden Funktionen zu zuordnen.



