So modellierst Du quadratische Funktionsgleichungen!

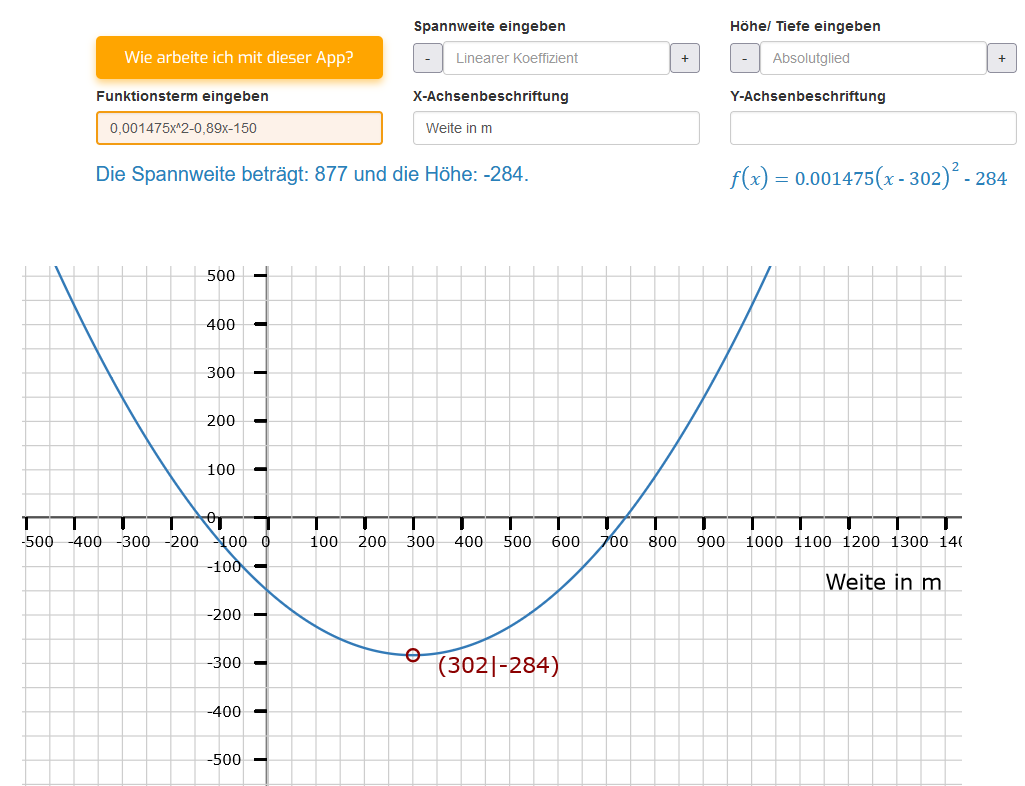
Es gibt zwei Typen von Modellierungsaufgaben. Im ersten Typ werden Spannweite und Höhe beziehungsweise Tiefe einer Parabelform genannt, dass kann zum Beispiel eine Brückenkonstruktion oder eine Flugbahn sein. Im zweiten Fall wird eine Funktionsgleichung vorgegeben, aus der man die Eckdaten, wie Spannweite und Scheitelpunkthöhe herleiten soll. Hier siehst Du nun eine bestimmte Einstellung unserer App, anhand der wir ihre Handhabung zur Lösung von Modellierungsaufgaben erklären werden.

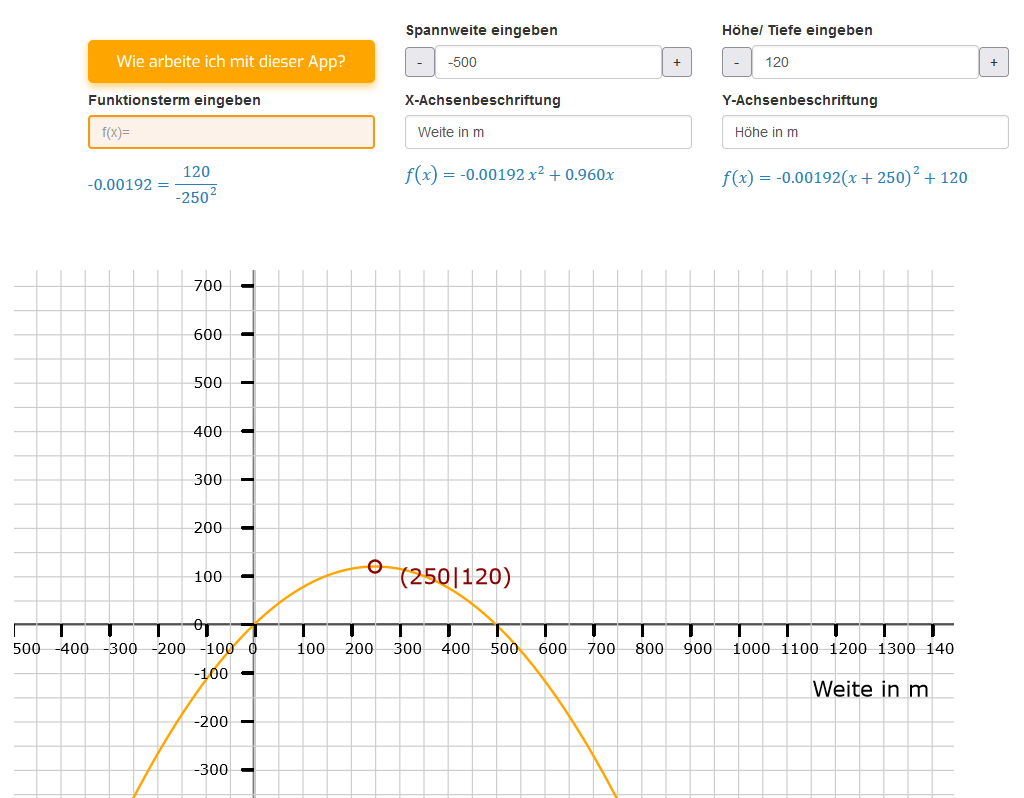
Handelt es sich um Anwendungsaufgaben des ersten Typs, so trägst Du in die Felder für Spannweite und Höhe bzw. Tiefe die Werte aus der Aufgabe ein. Im linken Bild geht es um die Erstellung der Funktionsgleichung aus der Spannweite und Höhe eines Brückenbogens. Dazu haben wir die Spannweite als negativen Wert eingetragen. Da es sich um einen Brückenbogen handelt, brauchen wir eine nach unten geöffnete Parabel. Da der Rechner den Streckfaktor aus der Höhe geteilt durch das Quadrat der halben Spannweite berechnet, brauchen wir den negativen Spannweitenwert, um einen negativen Streckfaktor zu erhalten. Entsprechend unserem Beispiel ist der Scheitelpunkt ein Hochpunkt, weswegen ein positiver Wert als Höhe eingetragen wird. Hier ist die Berechnungsformel für den Streckfaktor:

$\mathrm{-0,00192}=\frac{120}{-(250{)}^2}$. Dieser Streckfaktor wird vom Rechner übernommen, um jetzt sowohl die Normalform als auch die Scheitelpunktform der quadratischen Funktion anzuzeigen. Das fehlende Absolutglied in der Normalform zeigt an, dass der y-Achsenabschnitt im Ursprung liegt. Damit ist auch die erste Nullstelle gleich Null. In der Scheitelpunktform kann man wunderbar erkennen, dass für den y-Wert des Scheitelpunktes e 120 steht und für den x-Wert des Scheitelpunktes d 250. Wenn dieser Wert positiv ist, muss x einen negativen Wert annehmen, damit die binomische Formel zu Null wird. Folglich müsste die Parabel sich horizontal nach links verschieben. Sie verschiebt sich aber nach rechts. Der Grund dafür ist der negative Streckfaktor, der nach Ausmultiplizierung der binomischen Formel die Vorzeichen verkehrt.

Zusammen mit der Ausgabe der Funktionsgleichung wird die dazu gehörige Parabel geplottet. Dabei sehen wir in diesem Beispiel zunächst eine 1-er Skalierung, also nur den Anfang der Parabel. Mit dem Scrollrad der Maus oder 2 Fingern auf dem Tablet, können wir nun den Graph so weit auszoomen, dass die ganze Parabel sichtbar ist. Entsprechend des Zoomfaktors passt sich die Skalierung an. So sehen wir schließlich nebenstehendes Bild mit einer 100-er Skalierung.

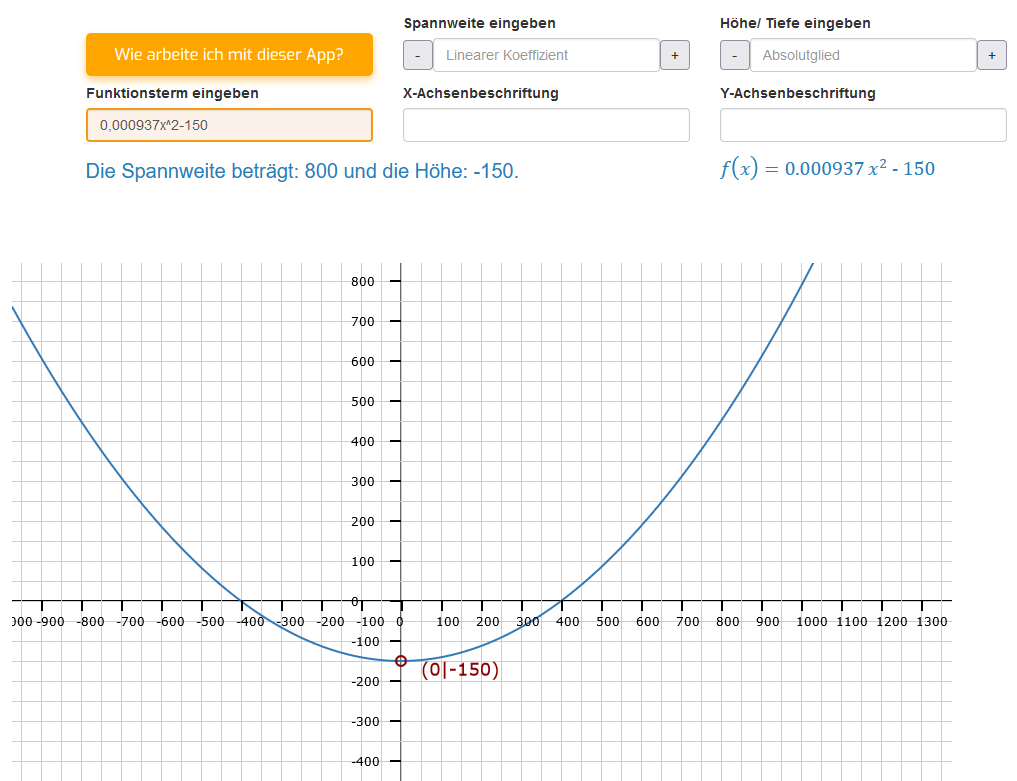
Im Bild rechts haben wir nun den Aufgabentyp 2. Es wurde eine quadratische Funktion vorgegeben, die in diesem Fall nur über den Streckfaktor und das Absolutglied verfügt. Aus diesen Angaben errechnet die App die Spannweite, das heißt den Abstand zwischen der ersten und zweiten Nullstelle und da der Koeffizient b fehlt, bildet die y-Achse die Spiegelachse der Parabel. Der Funktionsterm: $f\left(x\right)=\mathrm{0,000937}{x}^2-\mathrm{150}$ zeigt demnach eine stark gestauchte nach oben geöffnete Parabel. Der Scheitelpunkt ist daher hier ein Tiefpunkt und er befindet sich auf der y-Achse mit einem y-Wert von -150.

Über den Streckfaktor ermitteln wir die Spannweite. Dafür berechnen wir die Nullstellen aus der Normalform der Parabel: $f\left(x\right)=a{x}^2+c$. Hierfür setzen wir f(x) = 0 und erhalten: $$a{x}^2+c=0$$ Durch Umstellung erhalten wir:
$a{x}^2=-c$ ⇒ $x^2=-\frac{c}{a}$ ⇒ $x=\pm \sqrt{-\frac{c}{a}}$ für $-\frac{c}{a}\ge 0$.
Wenn wir jetzt die Parameter für a und c einsetzen, erhalten wir: $\mathrm{400}=\sqrt{\frac{150}{\mathrm{0,000937}}}$.
Da der Term unter der Wurzel größer Null ist, ist die Lösung für x₁ = 400 und für x₂ = -400. An der geplotteten Parabel im Bild kann man sehr gut erkennen, dass die Spanne zwischen -400 und 400 der angegebenen Spannweite von 800 entspricht. Im Gegensatz zum ersten Beispiel handelt es sich bei dieser Funktionsgleichung um eine nach oben geöffnete Parabel. Entsprechend ist der Scheitelpunkt ein Tiefpunkt und der y-Wert negativ. Das gewährleistet, dass es zwei Nullstellen gibt, ohne die eine Spannweitenberechnung nicht möglich ist.

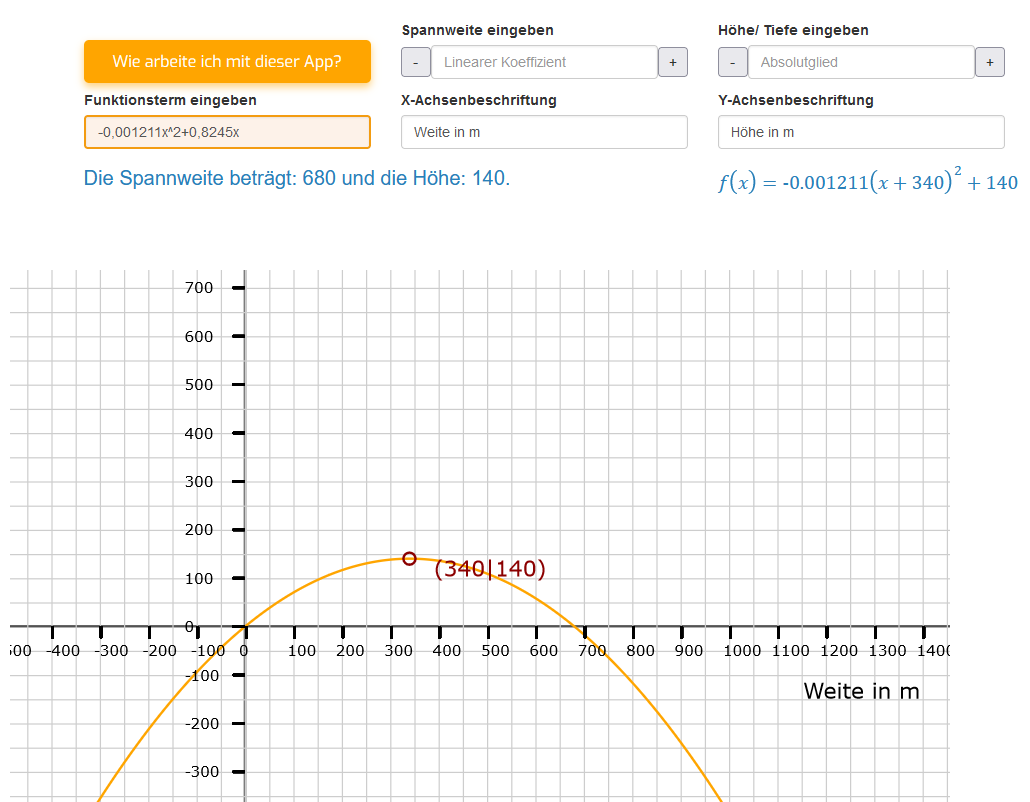
Wie im ersten Bild haben wir hier eine Parabel, deren erste Nullstelle durch den Ursprung geht, woran man sofort erkennen kann, dass das Absolutglied fehlt bzw. gleich Null ist. Folglich ist das der Funktionsterm: $$f\left(x\right)=-\mathrm{0,001211}{x}^2+\mathrm{0,8245}x$$.
Unter der Voraussetzung, dass wir den Koeffizienten b kennen und c = 0 ist, haben wir wiederum durch Umstellung des Funktionsterms folgende Berechnungsformel: $$a{x}^2+bx=0$$ Hier können wir x ausklammern, wodurch wir den Term faktorisieren, und erhalten: $$x(ax+b)=0$$ Nun setzen wir jeden der Faktoren gleich Null:
$x=<mn>0</mn>$
$ax+b=0$ ⇒ $x=-\frac{b}{a}$ und erhalten so als erste Nullstelle die Null und als zweite: $680=\frac{\mathrm{0,8245}}{\mathrm{0,001211}}$. Zur Ermittlung der Höhe nehmen wir die Hälfte der soeben ausgerechneten Spannweite, quadrieren sie und multiplizieren sie mit dem Streckfaktor: ${340}^2·\mathrm{0,001211}=140$. Durch diese quadratische Ergänzung haben wir die Normalform der Parabel in ihre Scheitelpunktform überführt. Siehe den Funktionsterm rechts oben.

Wenn wir im zweiten Bild eine Parabel sehen, deren Scheitelpunkt auf der y-Achse liegt, da das b fehlt, haben wir hier im rechten Bild nun eine Funktionsgleichung mit allen drei Parametern. Die Parabel ist somit gestaucht und sowohl vertikal als auch horizontal verschoben. Die errechnete Spannweite lässt sich an den Nullstellen gut ablesen. Der Funktionsterm: $$f\left(x\right)=\mathrm{0,001475}{x}^2-\mathrm{0,89}x-150$$.
Das Absolutglied $-150$ kannst Du an der Y-Achse als y-Achsenabschnitt ablesen. Wieder siehst du neben den Angaben für die Spannweite und die Höhe die Scheitelpunktform der Funktion. Wie schon oben wurde der Scheitelpunkt hier als roter Ring mit den Koordinaten für x und y eingestellt. Du kannst übrigens mit der Maus oder mit dem Finger einen beliebigen Punkt auf der Parabel auswählen und er wird entsprechend angezeigt. So kannst Du Scheitelpunkte, Nullstellen , y-Achsenabschnitte und beliebige andere Stellen auf der Parabel als Punkt mit Koordinaten anzeigen lassen.

Wie erstellst Du aus Spannweite und Höhe eine quadratische Funktionsgleichung?

In diesem Video wird eine quadratische Funktion zur Darstellung eines Flusstals modelliert. Der Fluss ist bei seinem normalen Pegelstand 100 Meter breit. Das Flusstal hat eine Weite von 1600 Metern. Die Talsenke, in deren Mitte der Fluss fließt, hat mit dem Pegelstand des Flusses einen Tiefpunkt von 35 Metern. Die Frage lautet, wieviel Meter Fläche des Tals links und rechts des Flusses überflutet werden, wenn der Pegelstand sich um 9 Meter erhöht. Dafür nehmen wir die Normalform der modellierten Parabel und setzen das Absolutglied auf 26 Meter. Dadurch wird die Parabel um 26 Meter angehoben und wir können im Plot an den neuen Nullstellen ablesen, dass links und rechts jeweils 350 Meter weit das Tal überflutet wird. Die Berechnungen und Darstellungen mit den Ausgaben der einzelnen Formen der Funktion wurden mit einer eigens dafür entwickelten App gemacht, die auch gut über ein Smartboard im Unterricht Verwendung finden kann.

Wie erstellst Du aus einer quadratischen Funktionsgleichung Spannweite und Höhe?

In diesem Video zeige ich, wie ich mithilfe meiner App die Werte einer typischen Modellierungsaufgabe für quadratische Funktionen in einen Funktionsterm umwandle. In unserem Beispiel soll die parabelförmige Form einer Bogenbrücke mit einer Spannweite von 800 Metern und dem höchsten Punkt von 50 Metern als Funktion dargestellt werden. Hierzu gebe ich die beiden Werte in die hierfür vorgesehenen Eingabefelder ein und drücke auf den Button, um die Parabel zu plotten. Als erstes wird die Formel angezeigt, wie der Streckfaktor aus der Spannweite und der Höhe berechnet wird. Weiterhin wird die Funktion in ihrer Normalform und ihrer Scheitelpunktform angezeigt. Auf der Zeichenfläche siehst du nun die eingezeichnete Parabel, jedoch nur ein kleines Stück von ihr. Durch Scrollen mit dem Mausrad zoomst du die Parabel soweit aus, bis du sie als Ganzes sehen kannst. Nun wurde auch die Skalierung mit 100-er Schritten angepasst. Mit einem Mausklick auf eine beliebige Stelle des Graphen kannst du dir Nullstellen, den Scheitelpunkt oder den y-Achsenabschnitt als runden Kreis mit den entsprechenden Koordinaten anzeigen lassen. Neben der Parabel wird die Berechnungsformel für den Streckfaktor gezeigt. Er wird aus der Höhe geteilt durch das Quadrat der halben Spannweite errechnet. Weiter kann man die Normalform und die Scheitelpunktform der Funktion sehen. Weiterhin wird gezeigt, wie der B-Koeffizient der Normalform aus dem Streckfaktor und der Spannweite berechnet wird.