So modellierst Du Exponentialfunktionen!
Die allgemeine Form der Exponentialfunktion lautet: . Sie kann bis zu 5 Parameter aufweisen. Wir beschäftigen uns hier aber nur mit den beiden Parametern b und a. Dadurch, dass der x-Wert im Exponenten steht, wird die Basiszahl a mit jeder Erhöhung von x um eins einmal mehr mit sich selbst multipliziert. Das führt zu einer zunehmend steiler wachsenden Kurve bei a > 1 oder zu einer zunehmend flacher fallenden Kurve bei a < 1. Die Basis muss ungleich eins sein, da 1 x immer eins ergibt und somit keinen exponentiellen Graphen.
Der Anfangswert b wird auch Streckfaktor genannt, da die Kurve umso steiler ansteigt, je höher der Wert von b ist. Dabei wird die Kurve bei b > 1 gestreckt und bei 0 < b < 1 gestaucht. b kann nicht den Wert Null annehmen. In Anwendungsaufgaben, auch Modellierungsaufgaben genannt, geht es meist um Wachstums- oder Zerfallsprozesse.
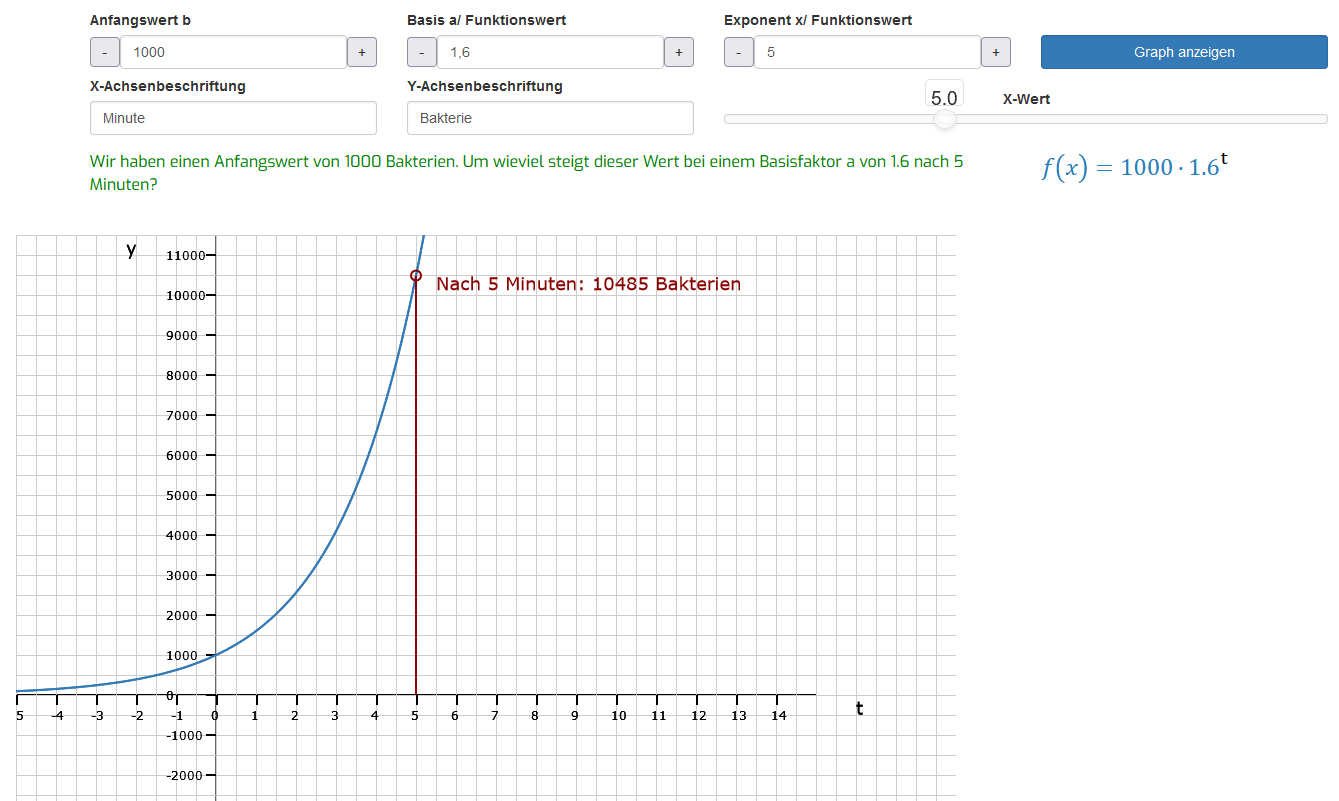
Im Bild links siehst Du die exponentiell wachsende Kurve aus einer typischen Anwendungsaufgabe. Es ist ein Anfangswert von 1000 Bakterien gegeben. Das entspricht unserem b. Weitere angegebene Werte sind die Basis a und der Zeitraum, über den ein Anstieg gemessen wird. In unserem Beispiel vermehren sich die Bakterien um das 1,6-fache ihres Anfangsbestandes innerhalb eines Zeitintervalls von 1 Minute. In der Aufgabe lautet die Fragestellung: Wieviele Bakterien gibt es nach 5 Minuten? Hierfür setzen wir jetzt als Exponenten x im 3. Eingabefenster eine 5 ein. Daraufhin wird in dieser App die entsprechende Funktionsgleichung angezeigt: . Der Ablesewert bei t = 5 liegt an der y-Achse bei 10485 Bakterien. Das ist die Anzahl, auf die der Anfangsbestand von 1000 Bakterien nach 5 Minuten gewachsen ist.
Du kannst jetzt mit dem Slider noch beliebige andere Werte einstellen, wirst aber sehen, dass schon nach 6 Minuten die Zahl so hoch ist, dass Du sie innerhalb der Grafik nicht mehr ablesen kannst.
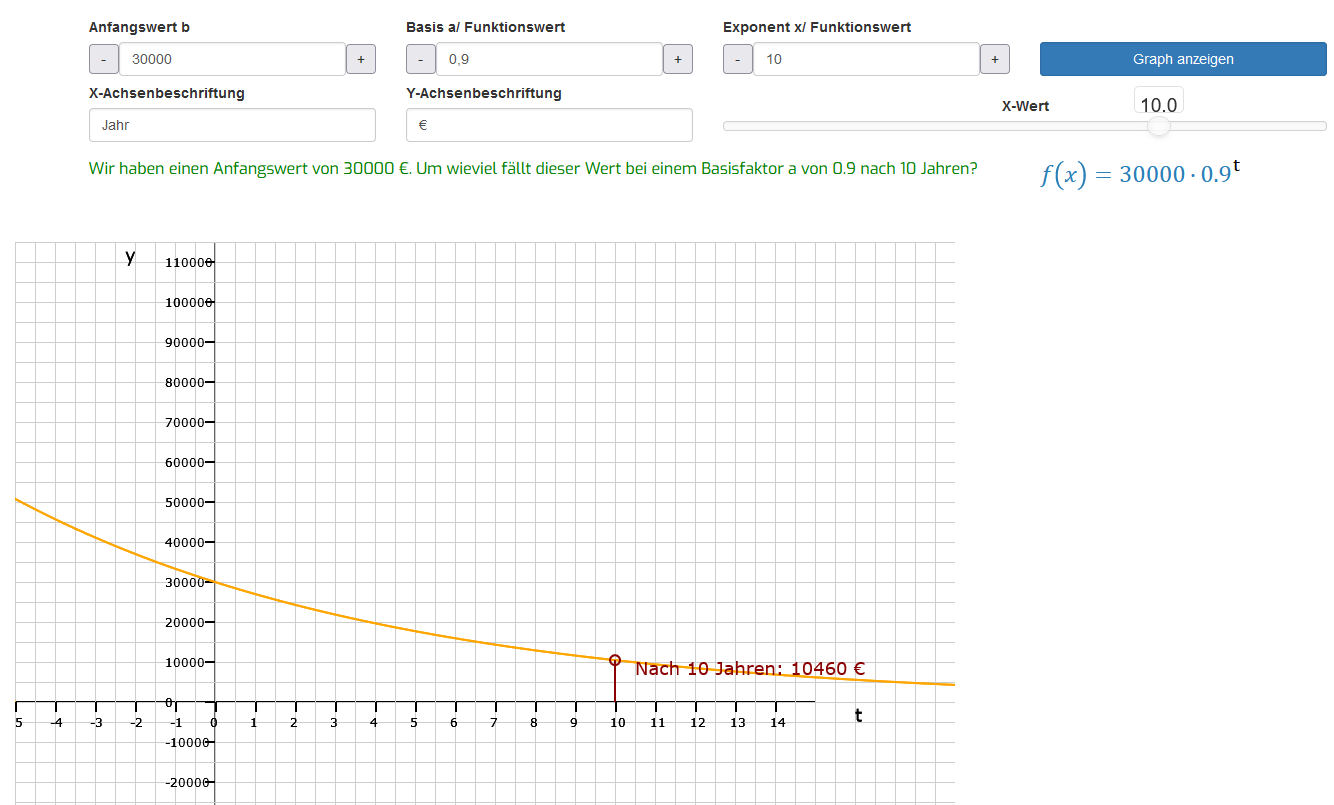
Im rechten Bild sehen wir die grafische Darstellung für einen Abnahmeprozess. Sehr häufig bewegen sich die Werte für die Basis a zwischen 1 und 2. Dann steht 1 für den Ausgangswert 100%. Jede Hundertstelstelle größer als 1 entspricht einer prozentualen Steigerung und jede Hundertstelstelle kleiner als 1 einem prozentualen Zerfall.
In diesem Beispiel gehen wir von einem Darlehen in Höhe von 30.000 € aus, das jährlich mit einer Tilgung von 10 % abgetragen werden soll. Die Frage lautet hier, wie hoch die Restschuld nach 10 Jahren ist.
Die Funktionsgleichung lautet hier: . Da es sich um eine exponentielle Abnahme von 10% handelt, ziehen wir von der Basis a 0,1 ab und rechnen bei einer 10-jährigen Laufzeit die 10-er Potenz von 0,9. Wir erhalten 10.460 € als noch zu tilgende Restsumme nach 10 Jahren.
Links siehst Du den Graph für eine ähnliche Aufgabe wie im ersten Bild, nur das diesmal anstatt der Angabe des Wachstumsfaktors a in das zweite Fenster der nach 3 Minuten gewachsene Endwert von 4650 eingegeben wird. Durch Umstellen der Funktionsgleichung erhalten wir und somit für a gerundet 1,669.
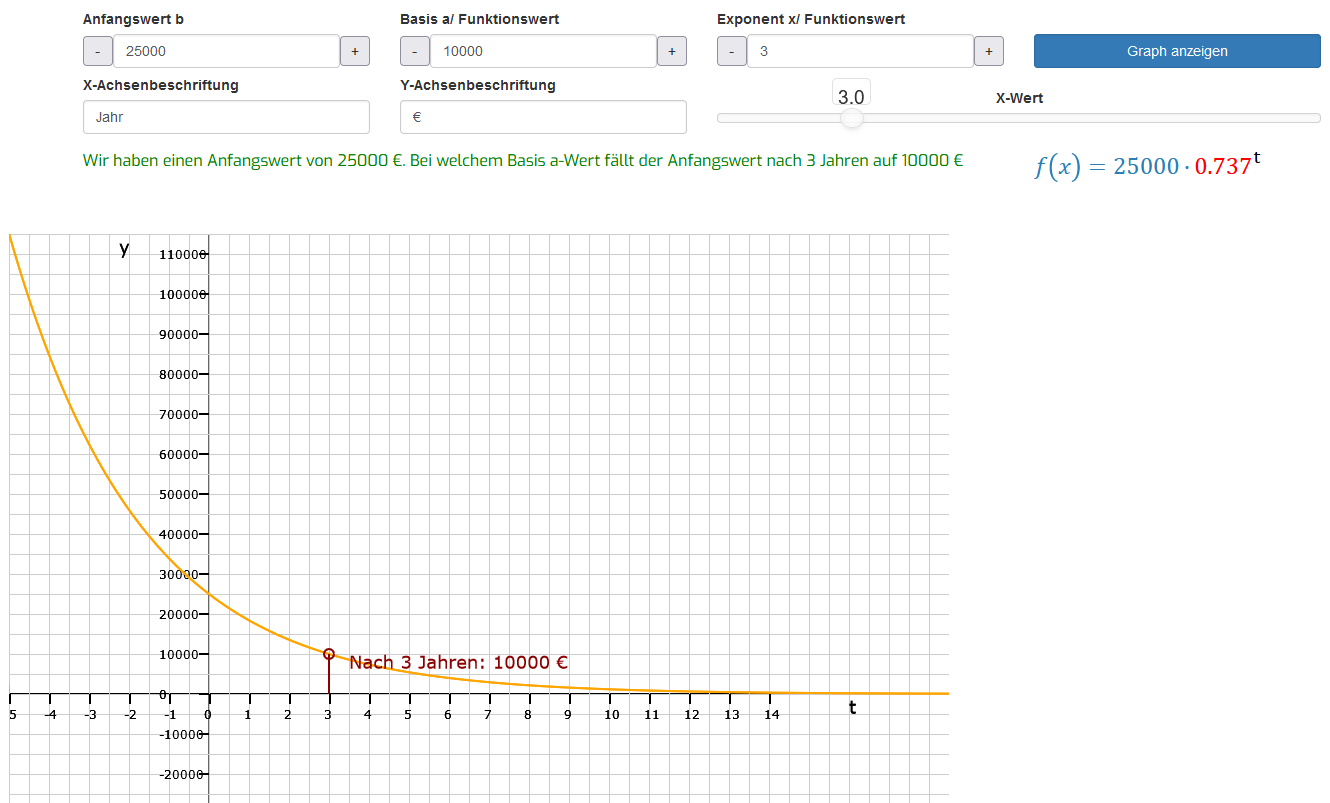
Das ganze funktioniert natürlich auch, wenn wir als Endwert eine niedrigere Zahl eingeben. Dadurch handelt es sich automatisch um eine Abnahme oder einen Zerfall. An der orangenen Kurve, die zusehends flacher werdend sinkt, sehen wir die Abnahme eines Anfangsbetrags von 25.000 €, erkennbar am y-Achsenabschnitt, auf 10.000 € nach 3 Jahren. Nach der Umstellung der Funktionsgleichung zur Berechnung von a erhalten wir gerundet den Wert 0,737. Also beträgt der Tilgungsfaktor hier26,3 %. Wichtig ist es zu erwähnen, dass der Endwert nie Null werden kann. Wenn x gegen unendlich geht, wird der y-Wert unendlich klein, erreicht aber nie die Null. Gibst Du als Funktionswert eine Null ein, zeigt das Programm eine Fehlermeldung.
