Die Exponentialfunktion mit ihren Veränderungsparametern!

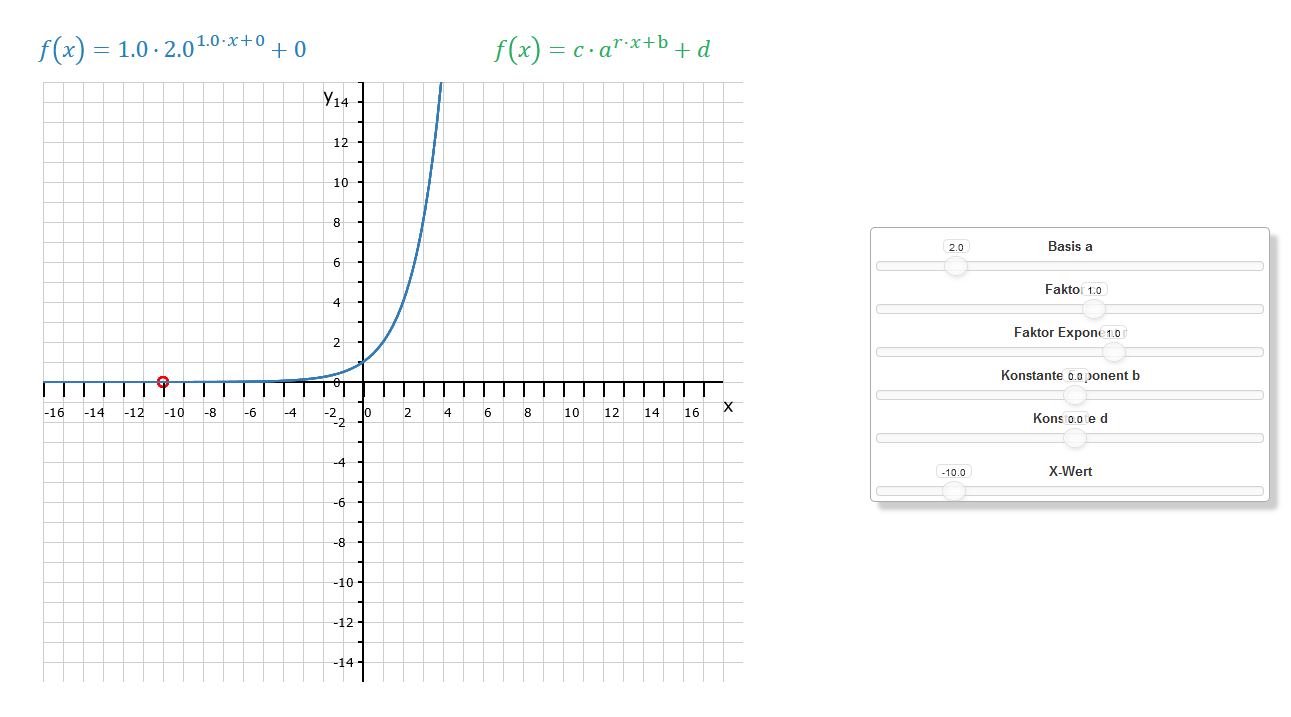
Die Standardform der Exponentialfunktion mit ihrer Basis a ist: $\mathrm{f(x)}=a^x$. Dabei ist, wie im nebenstehenden Bild zu sehen, a > 1. Der Exponent kann den Wert aller reelen Zahlen annehmen. Wenn x gegen +∞ strebt, strebt f(x) = a^x auch gegen +∞. Strebt hingegen x gegen -∞, so nähert sich die Kurve asymptotisch Null, das heißt, dass die x-Achse nie geschnitten wird. Der Grund dafür liegt darin, dass $\mathrm{f(x)}=a^{\mathrm{-x}}$ zu $\mathrm{f(x)}=\frac{1}{a^x}$ wird.

Im Koordinatensystem kann man das sehr gut sehen, dass der Funktionswert y im 2. Quadranten lange Zeit nahe Null ist und dann erst zwischen x = -4 und x = 0 steigt, um dann bei x = 0 den Wert 1 zu erhalten. Eine Exponentialfunktion ist unter den oben genannten Bedingungen immer stetig.

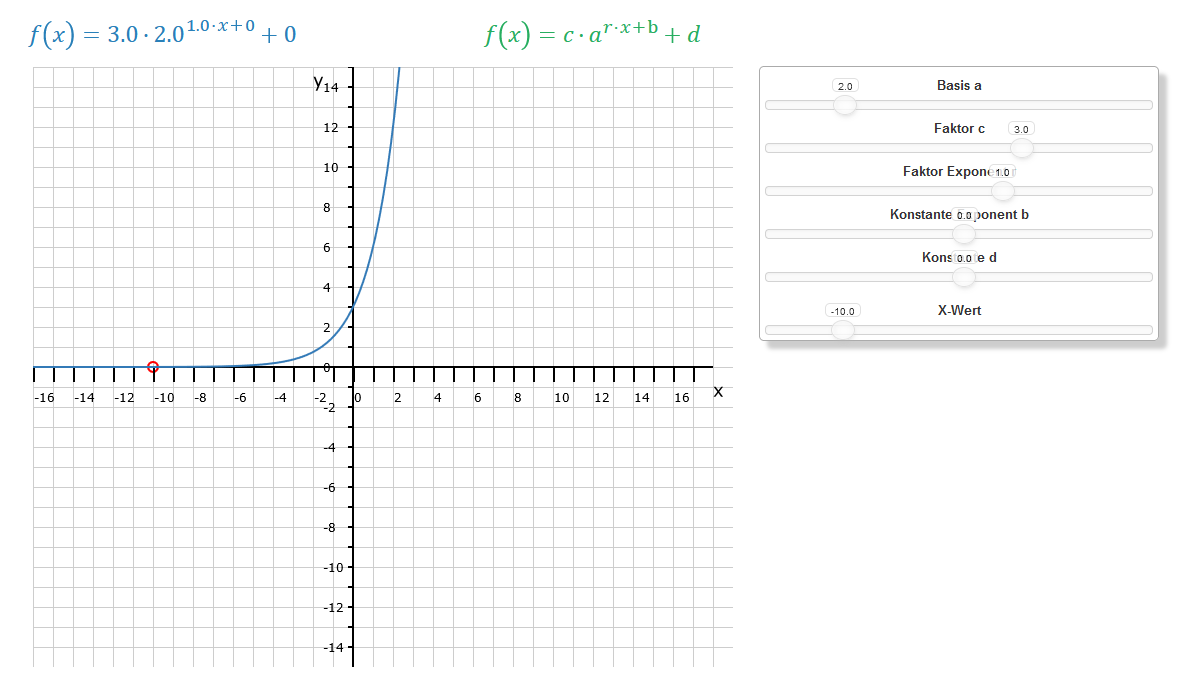
Eine Null im Exponenten ergibt mit jeder Basis immer 1. Das ändert sich erst, wenn der Koeffizient cins Spiel kommt. Wenn c ≠ 1 ist, dann ist sein Wert der Schnittpunkt auf der y-Achse, wie man im Bild links sehen kann.

Hier erhöht sich der Funktionswert immer um den Faktor 3. Der Faktor 3 in der Funktion $\mathrm{f(x)}=3·a^x$ sorgt für eine vertikale Streckung der Exponentialkurve und erhöht den y-Achsenabschnitt auf 3, hat aber keinen Einfluss auf die exponentielle Wachstums- oder Zerfallsrate der Funktion, die durch a^x bestimmt wird. Für eine Änderung der Steilheit sind die Parameter im Exponenten verantwortlich, auf die wir weiter unten zu sprechen kommen.

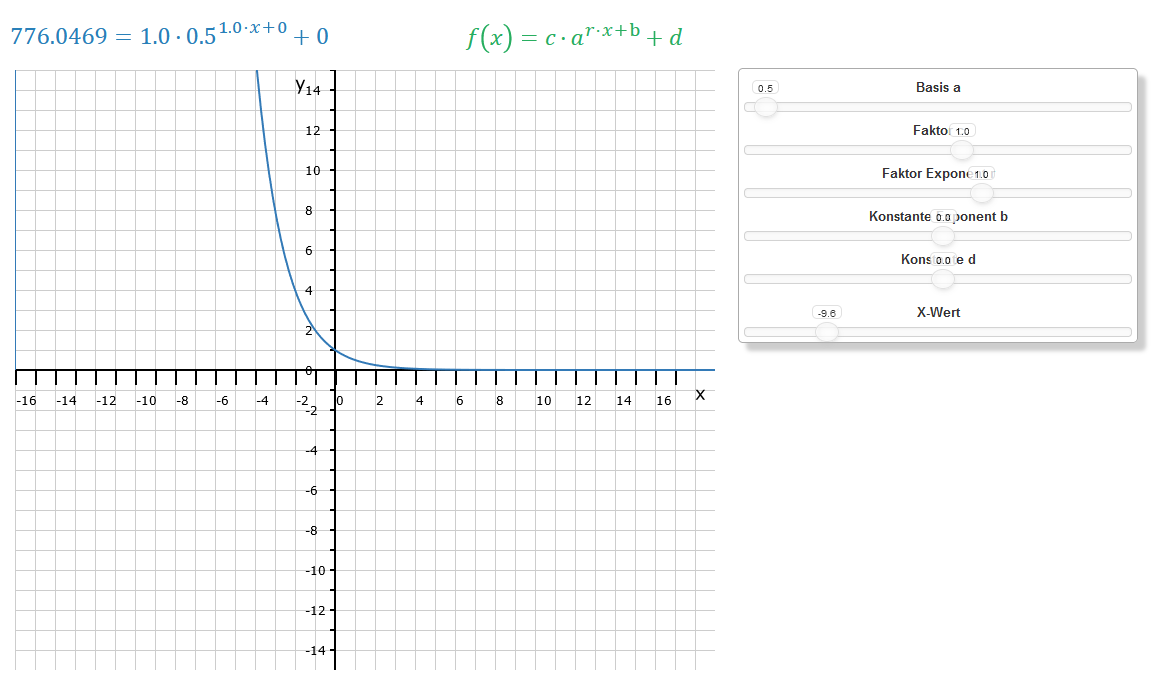
Im nebenstehenden Bild siehst Du eine Abbildung der Funktion: $\mathrm{f(x)}={\mathrm{0,5}}^x$. Steigt bei a > 1 die Kurve exponentiell, so fällt sie bei 0 < a < 1. Da in unserem Beispiel a = 0,5 ist und das der Kehrwert zu a = 2 ist, sind die beiden Funktionen: $\mathrm{f(x)}={\mathrm{0,5}}^x$ und $\mathrm{f(x)}=2^x$ achsensymmetrisch zueinander, und zwar bezüglich der y-Achse. Vergleiche dieses Bild mit dem ersten Bild oben.

Ist a größer 1, liegt immer eine exponentielle Steigung des Graphen bzw. eine exponentielle Zunahme des Funktionswertes y vor. Wenn der Wert von a zwischen Null und Eins liegt, nimmt der Funktionswert exponentiell ab. In Anwendungsaufgaben werden solche Funktionen häufig zur Beschreibung von Zerfallsprozessen verwendet, wobei a dann als prozentualer Faktor dient, der den Anteil des verbleibenden Materials oder der Substanz nach einer festgelegten Zeiteinheit angibt, und c der Anfangswert ist. a unterliegt den Einschränkungen a > 0 und a ≠ 0 . Ist 0 < a < 1, so handelt es sich um einen Zerfallsfaktor. Bei a > 1 spricht man vom Wachstumsfaktor.

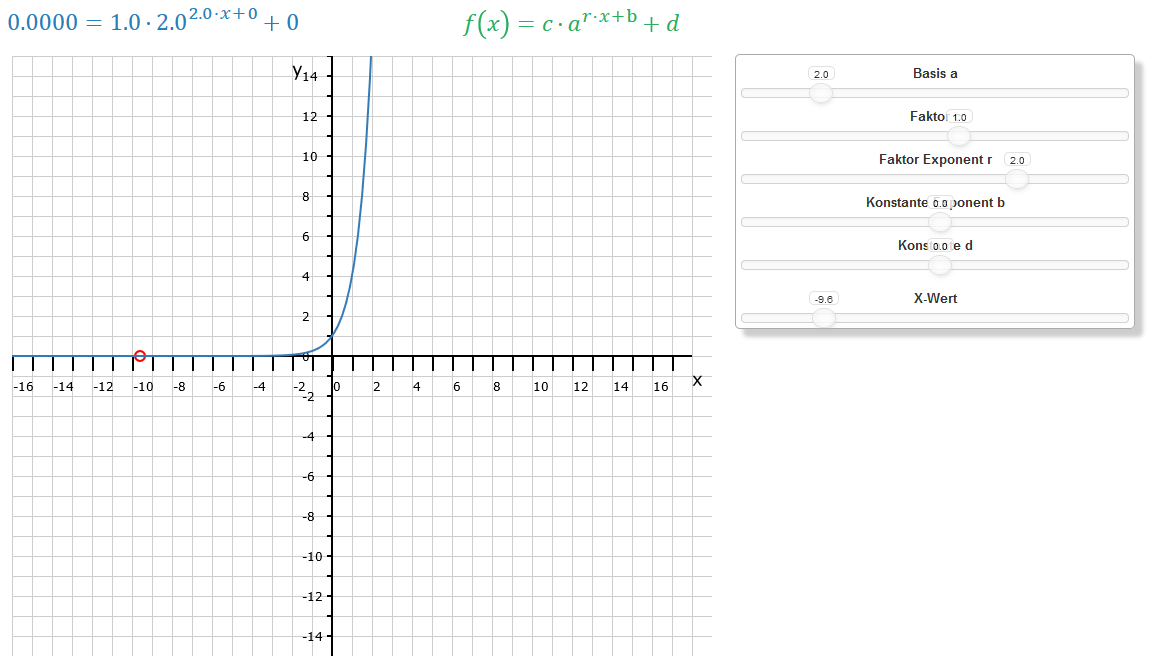
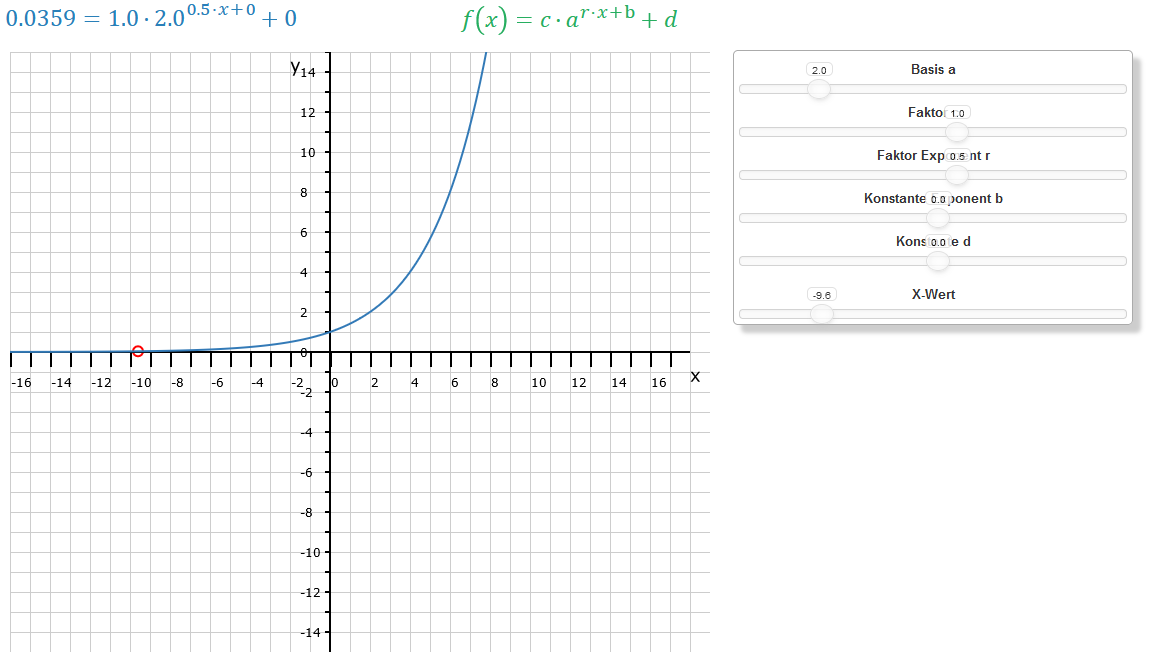
Wenden wir uns nun dem Faktor r zu. Dieser Koeffizient befindet sich im Exponenten einer Exponentialfunktion. Er beschleunigt bzw. bremst die Wachstums- oder Zerfallsrate. Dabei führen Werte zwischen Null und Eins zu einer flacheren Wachstums- oder Zerfallsrate und Werte größer 1 zu einer steileren. Gut kann man den Unterschied in den beiden Bildern links und rechts sehen. Im linken Bild führt die Funktion: $\mathrm{f(x)}=2^{2·x}$ zu einer steileren Kurve und $\mathrm{f(x)}=2^{\mathrm{0,5}·x}$ zu einer flacheren Kurve. Ein 0 < r < 1 führt demnach zu einer horizontalen Dehnung und ein r > 1 zu einer horizontalen Stauchung.

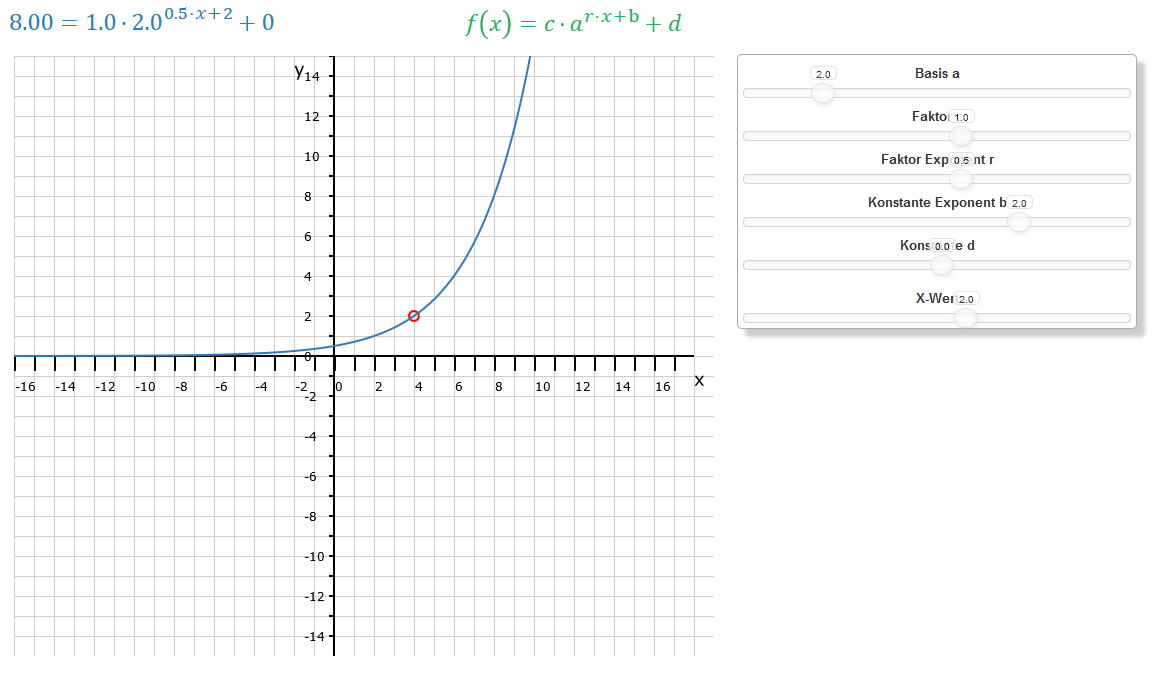
Im linken Bild haben wir den Parameter b auf 2 gesetzt. Er ist eine konstante Zahl, die zum Term der Funktion: $\mathrm{f(x)}=a^{\mathrm{0,5}·x+2}$ im Exponenten addiert wird. Er bewirkt eine horizontale Verschiebung der gesamten Exponentialfunktion. Wenn b positiv ist, verschiebt sich die Funktion nach links; ist b negativ, verschiebt sich die Funktion nach rechts.

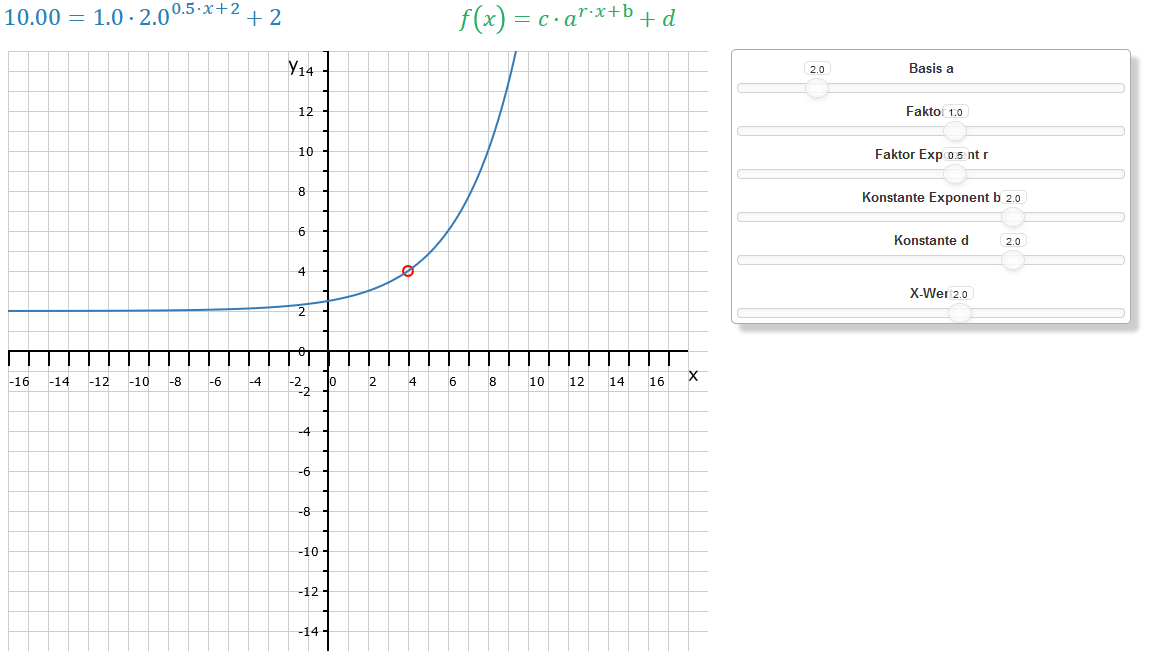
Im rechten Bild kommt nun noch der Parameter d hinzu. Diese konstante Zahl wird zum Funktionsterm addiert: $\mathrm{f(x)}=a^{\mathrm{0,5}·x+2}+2$. Er ist der vertikale Versatz (oder der y-Achsenabschnitt der gesamten Funktion). Er hebt oder senkt die gesamte Funktion um d Einheiten entlang der y-Achse.