Die Winkelfunktionen einfach erklärt am Einheitskreis!

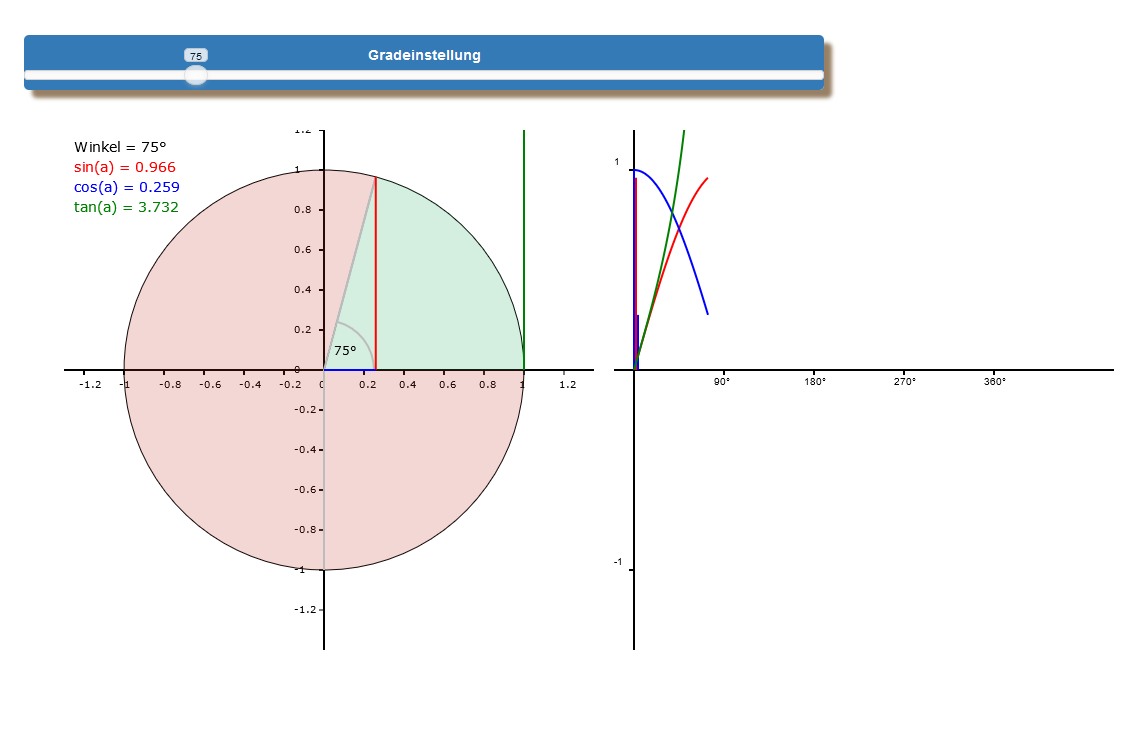
Im Gegensatz zu allen Funktionen, die wir bisher kennengelernt haben, ist der Graph einer Winkelfunktion eine sich periodisch wiederholende Welle. Um zu erklären, wie diese Welle zustande kommt, ist der Einheitskreis sehr hilfreich. Du siehst ihn hier links im Bild. Es handelt sich um einen Kreis mit dem Radius 1, dessen Mittelpunkt den Ursprung eines Koordinatensystems bildet. In unserer App können wir mithilfe eines Schiebereglers im Kreis gegen den Uhrzeigersinn einen Winkel öffnen. Dieses Öffnen lässt ein rechtwinkliges Dreieck entstehen, in dem der Radius die Hypotenuse bildet, die blaue Seite die Ankathete und die rote Seite die Gegenkathete.

Der Winkel lässt sich so bis maximal 360° öffnen. Dann beginnt der gleiche Ablauf von vorne. Eine solche Umrundung nennt man Periode. Was passiert in dieser Periode? Dadurch, dass der Radius des Einheitskreises eins ist, ist die Hypotenuse stets gleich lang und je nach Winkelgröße verkürzt oder verlängert sich die Länge von Ankathete und Gegenkathete. Dabei bildet die Länge der Gegenkathete den Sinuswert und die Länge der Ankathete den Kosinuswert. In dem Applet kannst Du nun durch Betätigen des Schiebereglers sehr gut erkennen, dass sich das Längenverhältnis von Gegenkathete und Ankathete ständig verändert, aber den Wert von 1 aufgrund des Radius von 1 nie überschreiten kann.

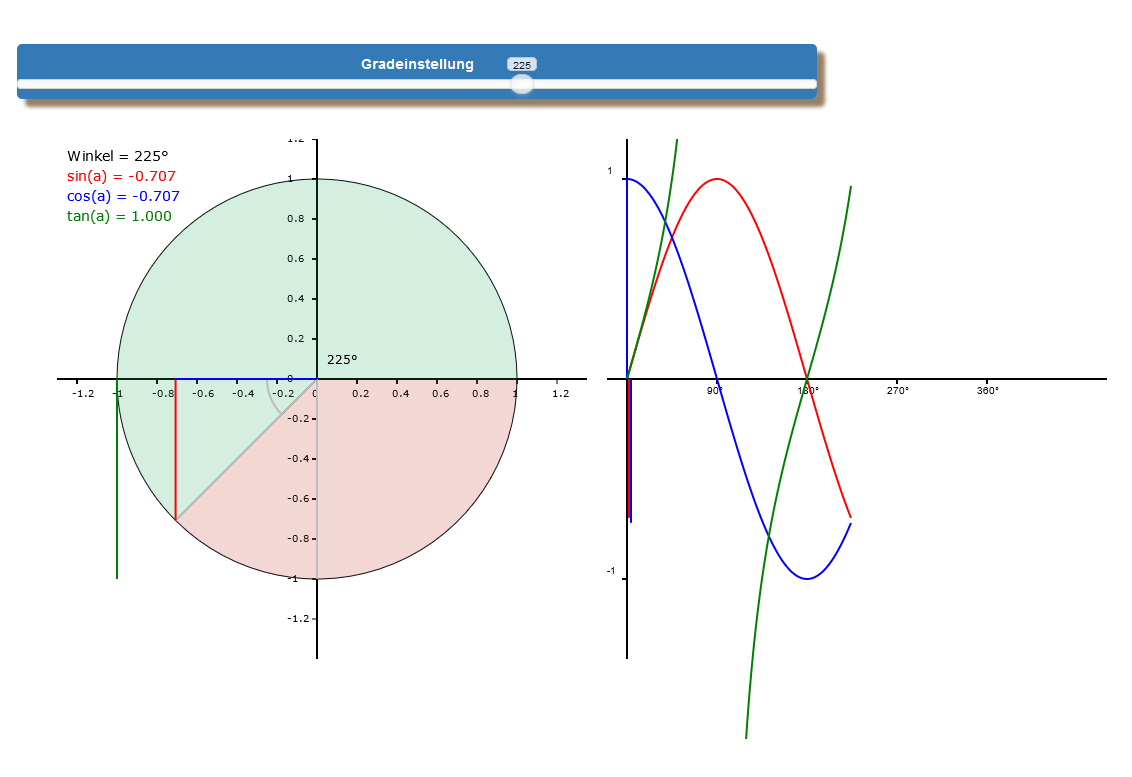
In der Legende links oben kannst Du nun die Längen der beiden Kathetenseiten bei einem bestimmten Winkel als Sinuswert bzw. Kosinuswert ablesen. Bei 0° existiert das Dreieck noch nicht. Es besteht nur aus der Ankathete, die folglich die Radiuslänge 1 hat. Mit jedem Grad mehr schrumpft die Länge der Ankathete und die Gegenkathete entsteht und nimmt an Länge zu, bis wir bei 90° angelangt sind, wo jetzt die Gegenkathete die Radiuslänge hat und die Ankathete verschwunden ist.

Das ist die Erklärung dafür, dass der Sinuswert bei Null beginnt und der Kosinuswert bei eins. Nun haben wir aber noch eine andere, grüne Linie, die auch Änderungen unterliegt. Es ist der Tangens. Er berührt den Einheitskreis und bildet die Gegenkathete eines Dreiecks, dessen Ankathete der Radius des Einheitskreises ist und die Hypotenuse über den Einheitskreis hinausgeht und deren Linie wir uns weiter denken müssen, bis sie sich mit dem Ende des Tangens trifft. Gut kann man das im nebenstehenden Bild sehen. Das bedingt, dass der Tangens bis 89° wächst, bei 90° gegen unendlich geht und ab 91° den gleichen Wert wie bei 89° hat, nur negativ, da wir uns jetzt im 2. Quadranten des Koordinatensystems befinden. Dieser Wert sinkt wieder gegen Null, der bei 180° erreicht wird.

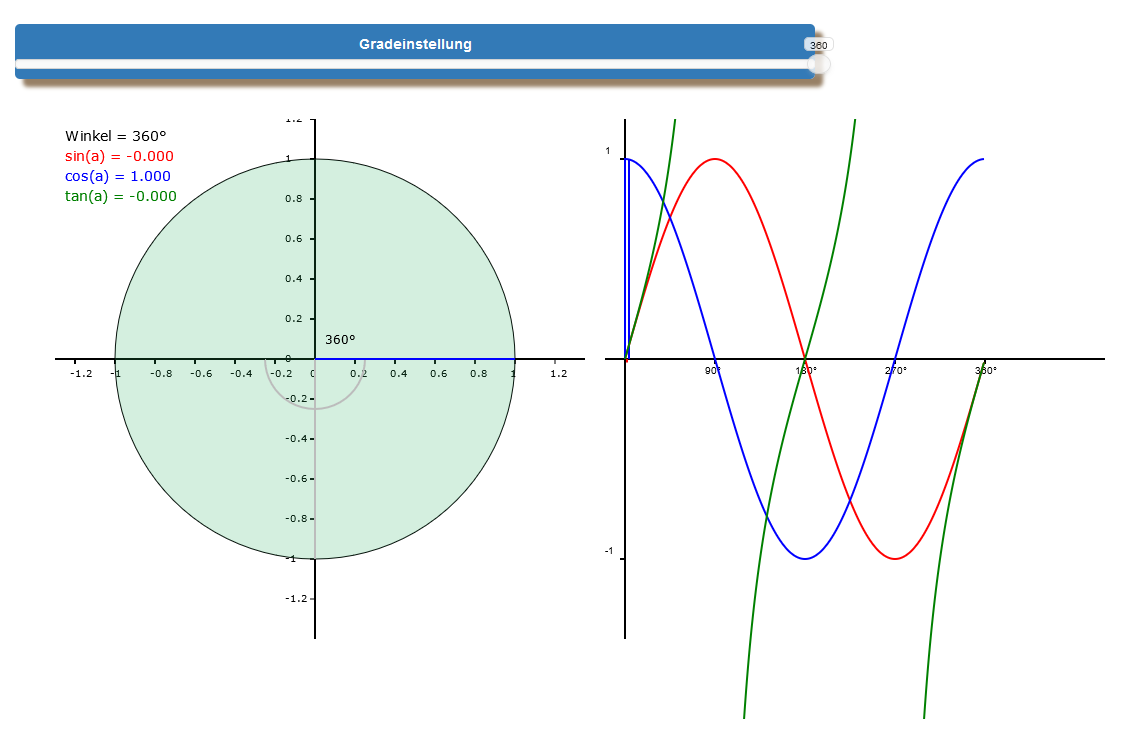
Nun kommen wir zu den eigentlichen Funktionsgraphen. Alle oben beschriebenen Vorgänge bilden wir nun entlang der x-Achse ab. Ihre Skalierung ist die Gradzahl. Die rote wellenförmige Kurve entsteht durch die Aneinanderreihung von Punkten, die aus den Koordinaten Gradzahl und Länge der Gegenkathete ihre Position erhalten. Aus ihnen entsteht die Sinuskurve. Sie beginnt im Ursprung, beschreibt einen Bogen bis 90°, senkt sich dann wieder und hat ihre erste Nullstelle bei 180°. Danach sinkt sie weiter, hat ihren Tiefpunkt bei -1 bzw. 270° und schließlich ihre zweite Nullstelle bei 360°. Diesen Verlauf von 0° bis 360° nennt man Periode. Dabei hat die Periode eine Länge von 2 π, das ist der Umfang des Einheitskreises, der sich aus U = 2 · r · π berechnet.

Die blaue Kosinuskurve hat den gleichen Verlauf wie die rote Sinuskurve, nur dass sie nicht bei null, sondern bei eins beginnt. Das führt dazu, dass sie gegenüber der Sinuskurve um $\frac{\pi }{4}$ nach links verschoben ist. Die charakteristische Linienführung des Tangens resultiert aus dem oben beschriebenen Umstand, dasss die Werte bis 90° bzw. 270° gegen positiv unendlich gehen und bis 180° bzw. 360° von negativ unendlich kommend nach null gehen.